【题目】如图，在边长均为1的正方形网格纸上有一个△ABC，顶点A、B、C及点O均在格点上，请按要求完成以下操作或运算：

（1）将△ABC向上平移4个单位，得到△A1B1C1（不写作法，但要标出字母）；
（2）将△ABC绕点O旋转180°，得到△A2B2C2（不写作法，但要标出字母）；
（3）求点A绕着点O旋转到点A2所经过的路径长．

参考答案：

【答案】
（1）解：△A1B1C1如图所示；


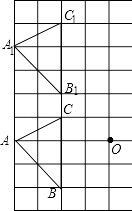
（2）解：△A2B2C2如图所示：


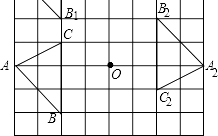
（3）解：∵OA=4，∠AOA2=180°，

∴点A绕着点O旋转到点A2所经过的路径长为 =4π．


【解析】（1）根据图形平移的性质画出平移后的△A1B1C1即可；（2）根据图形旋转的性质画出△ABC绕点O旋转180°后得到的△A2B2C2；（3）根据弧长的计算公式列式即可求解．

关闭