Question

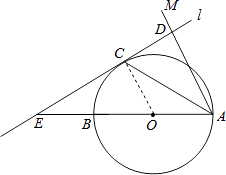
【题目】如图，AB为⊙O的直径，点C为⊙O上一点，若∠BAC=∠CAM，过点C作直线l垂直于射线AM，垂足为点D．
（1）试判断CD与⊙O的位置关系，并说明理由；
（2）若直线l与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°，求CE的长．

Answer 1

【答案】
（1）解：直线CD与⊙O相切．

理由如下：连接OC．

∵OA=OC，

∴∠BAC=∠OCA，

∵∠BAC=∠CAM，

∴∠OCA=∠CAM，

∴OC∥AM，

∵CD⊥AM，

∴OC⊥CD，

∵OC为半径，

∴直线CD与⊙O相切．

（2）解：∵OC=OA，

∴∠BAC=∠ACO，

∵∠CAB=30°，

∴∠COE=2∠CAB=60°，

∴在Rt△COE中，OC=3，CE=OCtan60°= ．

【解析】（1）连接OC，根据OA=OC，推出∠BAC=∠OCA，求出∠OCA=∠CAM，推出OC∥AM，求出OC⊥CD，根据切线的判定推出即可；（2）根据OC=OA推出∠BAC=∠ACO，求出∠COE=2∠CAB=60°，在Rt△COE中，根据CE=OCtan60°求出即可．
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识，掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线，以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．