搜索
【题目】在△ABC中，AB=AC=10，cosB= 
，如果圆O的半径为2 
，且经过点B、C，那么线段AO的长等于 ．
参考答案：
【答案】6或10
【解析】解：作AD⊥BC于D，如图， ∵AB=AC，
∴AD垂直平分BC，
∴点O在AD上，连接OB，如图，
在Rt△ABD中，cosB= 
= 
，
∴BD=10× =6，
∴AD= 
=8，
在Rt△BOD中，OD= 
=2，
∴OA=AD﹣OD=8﹣2=6．
或OA=AD+OD=8+2=10．
所以答案是6或10．
【考点精析】关于本题考查的等腰三角形的性质和垂径定理，需要了解等腰三角形的两个底角相等（简称：等边对等角）；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校准备在七年级举办百科知识竞赛,在张贴规则宣传之后,为了解学生对这次竞赛的了解程度,在全校400名七年级学生中随机抽取部分学生迸行了一次问卷调查，并根据收集到的信息进行了统计，绘制了下面两幅统计图.
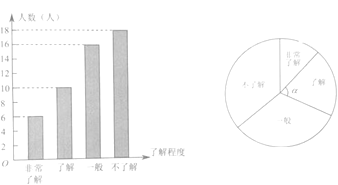
(1)抽取调查的学生人数是_____人;
(2)扇形统计图中“了解”对应的圆心角α的度数是_____度;
(3)全校七年级学生中对这次竞赛“非常了解”的大约有 人。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB=
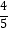，反比例函数y= 
在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于（ ） 
A.60
B.80
C.30
D.40 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC中，AB=AC，过边AB上一点N作AB的垂线交BC于点M．
（1）如图1，若∠A=40°，求∠NMB的度数．
（2）如图2，若∠A=70°，求∠NMB的度数．
（3）你可以再分别给出几个∠A（∠A为锐角）的度数，你发现规律了吗？写出当∠A为锐角时，你猜想出的规律，并进行证明．
（4）当∠A为直角、钝角时，是否还有（3）中的结论（直接写出答案）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】海洋馆的门票价格规定如表：
购票人数(人)
150人
51100人
100人以上
门票单价(元/人)
60
55
50
某校七年级一、二两班共102人去游公园，其中一班人数较多，经计算，如果两班都以班为单位分别购买与实际人数相同的票，则一共应付5850元。
请根据以上信息解答下列问题：
①两班各有多少学生?
②如果两班作为一个团体购票，可以节省多少钱?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF延长交AC于点E．若AB=10，BC=16，则线段EF的长为 ．
-
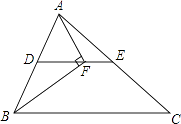
科目： 来源： 题型：
查看答案和解析>>【题目】我国著名数学家华罗庚曾经说过，“数形结合百般好，隔裂分家万事非。”数形结合的思想方法在数学中应用极为广泛.
观察下列按照一定规律堆砌的钢管的横截面图：
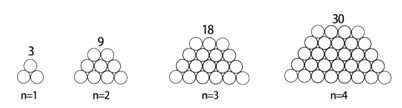
用含n的式子表示第n个图的钢管总数.
（分析思路）
图形规律中暗含数字规律，我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律。
如:要解决上面问题，我们不妨先从特例入手:(统一用S表示钢管总数)
（解决问题）
(1)如图，如果把每个图形按照它的行来分割观察，你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.
S=1+2 S=2+3+4 _____________ ______________
(2)其实，对同一个图形，我们的分析眼光可以是不同的。请你像(1)那样保持结构的、对每一个所给图形添加分割线，提供与(1)不同的分割方式;并在所给横线上，请用数学算式表达你发现的规律:
_______ ____________ _______________ _______________
(3)用含n的式子列式，并计算第n个图的钢管总数.
相关试题
