【题目】已知△ABC中,AB=AC,过边AB上一点N作AB的垂线交BC于点M.
(1)如图1,若∠A=40°,求∠NMB的度数.
(2)如图2,若∠A=70°,求∠NMB的度数.
(3)你可以再分别给出几个∠A(∠A为锐角)的度数,你发现规律了吗?写出当∠A为锐角时,你猜想出的规律,并进行证明.
(4)当∠A为直角、钝角时,是否还有(3)中的结论(直接写出答案).

参考答案:
【答案】(1)20°;(2)35°;(3)∠NMB=![]() ∠A,理由见解析;(4)当∠A为直角、钝角时,(3)中的结论仍然成立.
∠A,理由见解析;(4)当∠A为直角、钝角时,(3)中的结论仍然成立.
【解析】
(1)利用等边对等角求出∠B,在直角△BNM中即可求解,
(2)利用等边对等角求出∠B,在直角△BNM中即可求解,
(3)总结前两问,找到规律即可解题,
(4)代入角度求值,验证结论即可.
(1)∵AB=AC,∠A=40°,
∴∠B=∠C=![]() ×(180°-40°)=70°,
×(180°-40°)=70°,
∵MN⊥AB,
∴∠MNB=90°,
∴∠NMB=90°-∠B=20°,
故答案为:20°;
(2)∵AB=AC,∠A=70°,
∴∠B=∠C=![]() ×(180°-70°)=55°,
×(180°-70°)=55°,
∵MN⊥AB,
∴∠MNB=90°,
∴∠NMB=90°-∠B=35°,
故答案为:35°;
(3)∠A=40°时,∠NMB=20°,∠NMB=![]() ∠A,
∠A,
∠A=70°时,∠NMB=35°,∠NMB=![]() ∠A,
∠A,
∴∠NMB=![]() ∠A,
∠A,
理由如下:∵AB=AC,
∴∠B=∠C=![]() ×(180°-∠A)=90°-
×(180°-∠A)=90°-![]() ∠A,
∠A,
∵MN⊥AB,
∴∠MNB=90°,
∴∠NMB=90°-∠B=90°-(90°-![]() ∠A)=
∠A)=![]() ∠A;
∠A;
(4)当∠A=90°时,∠B=∠C=45°,
∴∠NMB=90°-45°=![]() ∠A,
∠A,
当∠A=100°时,∠B=∠C=40°,
∴∠NMB=90°-50°=![]() ∠A,
∠A,
则当∠A为直角、钝角时,(3)中的结论仍然成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于点E,在AC边取点D,使∠CBD=20°,连接DE,则∠CED的大小=_____(度).
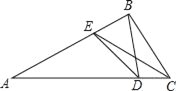
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备在七年级举办百科知识竞赛,在张贴规则宣传之后,为了解学生对这次竞赛的了解程度,在全校400名七年级学生中随机抽取部分学生迸行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.
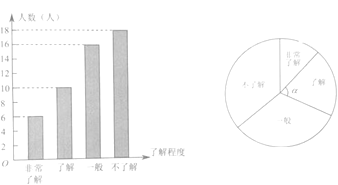
(1)抽取调查的学生人数是_____人;
(2)扇形统计图中“了解”对应的圆心角α的度数是_____度;
(3)全校七年级学生中对这次竞赛“非常了解”的大约有 人。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
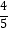 ,反比例函数y=
,反比例函数y=  在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 
A.60
B.80
C.30
D.40 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=10,cosB=
 ,如果圆O的半径为2
,如果圆O的半径为2 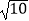 ,且经过点B、C,那么线段AO的长等于 .
,且经过点B、C,那么线段AO的长等于 . -
科目: 来源: 题型:
查看答案和解析>>【题目】海洋馆的门票价格规定如表:
购票人数(人)
150人
51100人
100人以上
门票单价(元/人)
60
55
50
某校七年级一、二两班共102人去游公园,其中一班人数较多,经计算,如果两班都以班为单位分别购买与实际人数相同的票,则一共应付5850元。
请根据以上信息解答下列问题:
①两班各有多少学生?
②如果两班作为一个团体购票,可以节省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为 .
相关试题

