【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:
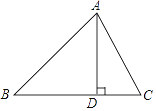
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,列出方程求出x→再求出AD的长,从而计算三角形的面积.请你按照他们的解题思路完成解答过程.
参考答案:
【答案】84
【解析】
直接利用BC的长表示出DC的长,再利用勾股定理进而得出x的值,然后利用三角形面积求法得出答案;
在△ABC中,AB=15,BC=14,AC=13, 设BD=x,则有CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2 , AD2=AC2﹣CD2=132﹣(14﹣x)2
∴152﹣x2=132﹣(14﹣x)2 ,
解之得:x=9,
∴AD=12,
∴S△ABC=![]() BCAD=
BCAD=![]() ×14×12=84
×14×12=84
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以
 ,
,  ,
,  的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以
 ,
,  ,
,  的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形其中所有正确结论的序号为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(1﹣2k)x2﹣2
 x﹣1=0
x﹣1=0(1)若此方程为一元一次方程,求k的值.
(2)若此方程为一元二次方程,且有实数根,试求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将函数y=x2﹣2x(x≥0)的图象沿y轴翻折得到一个新的图象,前后两个图象其实就是函数y=x2﹣2|x|的图象.
(1)观察思考
函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;方程x2﹣2|x|=2有 个实数根;关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 ;
(2)拓展探究
①如图2,将直线y=x+1向下平移b个单位,与y=x2﹣2|x|的图象有三个交点,求b的值;
②如图3,将直线y=kx(k>0)绕着原点旋转,与y=x2﹣2|x|的图象交于A、B两点(A左B右),直线x=1上有一点P,在直线y=kx(k>0)旋转的过程中,是否存在某一时刻,△PAB是一个以AB为斜边的等腰直角三角形(点P、A、B按顺时针方向排列).若存在,请求出k值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 相交于点
相交于点 ,
, ,点
,点 是直线上的一个定点,点
是直线上的一个定点,点 在直线
在直线 上运动,若以点
上运动,若以点 ,
, ,
, 为顶点的三角形是等腰三角形,则
为顶点的三角形是等腰三角形,则 的度数是__________.
的度数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
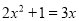 (配方法)
(配方法) (2)
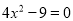 (因式分解法)
(因式分解法) (3)
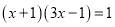 ( 公式法)
( 公式法)
相关试题

