【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论的序号为______.
参考答案:
【答案】②③.
【解析】解:(1)直角三角形的三条边满足勾股定理a2+b2=c2,因而以a2,b2,c2的长为边的三条线段不能满足两边之和>第三边,故不能组成一个三角形,故错误;
(2)直角三角形的三边有a+b>c(a,b,c中c最大),而在![]() ,
, ![]() ,
, ![]() 三个数中
三个数中![]() 最大,如果能组成一个三角形,则有
最大,如果能组成一个三角形,则有![]() +
+![]() >
>![]() 成立,即
成立,即![]() ,即
,即![]() ,(由a+b>c),则不等式成立,从而满足两边之和>第三边,则以
,(由a+b>c),则不等式成立,从而满足两边之和>第三边,则以![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形,故正确;
的长为边的三条线段能组成一个三角形,故正确;
(3)a+b,c+h,h这三个数中c+h一定最大,(a+b)2+h2=a2+b2+2ab+h2,(c+h)2=c2+h2+2ch
又∵2ab=2ch=4S△ABC
∴(a+b)2+h2=(c+h)2,根据勾股定理的逆定理
即以a+b,c+h,h的长为边的三条线段能组成直角三角形.故正确;
(4)若以![]() ,
, ![]() ,
, ![]() 的长为边的3条线段能组成直角三角形,假设a=3,b=4,c=5.∵(
的长为边的3条线段能组成直角三角形,假设a=3,b=4,c=5.∵(![]() )2+(
)2+(![]() )2≠(
)2≠(![]() )2,∴以这三个数的长为线段不能组成直角三角形,故错误.
)2,∴以这三个数的长为线段不能组成直角三角形,故错误.
故答案为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠BAC=60°,点P为边BC的中点,分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE,且∠DAB=∠EAC=α,连结PD,PE,DE.
(1)如图1,若α=45°,则
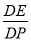 = ;
= ;(2)如图2,若α为任意角度,求证:∠PDE=α;
(3)如图3,若α=15°,AB=8,AC=6,则△PDE的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,并观察下列两个代数式的值的变化情况。

(2)随着n的值逐渐变大,两个代数式的值如何变化?
(3)估计一下,哪个代数式的值先超过100?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(1﹣2k)x2﹣2
 x﹣1=0
x﹣1=0(1)若此方程为一元一次方程,求k的值.
(2)若此方程为一元二次方程,且有实数根,试求k的取值范围.
-
科目: 来源: 题型:
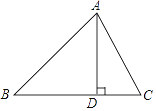
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路:
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,列出方程求出x→再求出AD的长,从而计算三角形的面积.请你按照他们的解题思路完成解答过程.
相关试题

