【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=2,求EF的长.

参考答案:
【答案】(1)详见解析;(2)EF=![]()
【解析】
(1)由已知条件不难证明△ADC≌△BDG,可得BG=AC,∠CAD=∠GBD,由E,F分别是BG,AC的中点可得ED=![]() BG,DF=
BG,DF=![]() AC,进而得出ED=DF=BE=EG=AF=CF,所以△BED≌△AFD,所以∠BDE=∠ADF,所以∠ADF+∠EDA=90°即DE⊥DF;(2)由AC的长度可得出DE、DF的长度,由勾股定理求出EF的长度即可.
AC,进而得出ED=DF=BE=EG=AF=CF,所以△BED≌△AFD,所以∠BDE=∠ADF,所以∠ADF+∠EDA=90°即DE⊥DF;(2)由AC的长度可得出DE、DF的长度,由勾股定理求出EF的长度即可.
(1)∵AD⊥BC,
∴∠ADC=∠BDG=90°,
∵在△ADC与△BDG中,
 ,
,
∴△ADC≌△BDG,
∴BG=AC,∠CAD=∠GBD,
∵AD⊥BC,E,F分别是BG,AC的中点,
∴BE=EG,AF=CF,ED=![]() BG,DF=
BG,DF=![]() AC,
AC,
∴ED=DF=BE=EG=AF=CF,
∵在△BED与△AFD中,
 ,
,
∴△BED≌△AFD,
∴∠BDE=∠ADF,
∵∠BDE+∠EDA=90°,
∴∠ADF+∠EDA=90°,
∴DE⊥DF;
(2)连接EF,由(1)得△DEF为等腰直角三角形,
∵AC=2,
∴DE=DF=1,
∴EF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第
 s或
s或 s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣1(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴交于点C.

(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3)点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2
 =(1+
=(1+ )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.(2)若a+4
 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 , C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=
 ,则AF的长度为( )
,则AF的长度为( ) 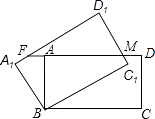
A.2﹣
B.
C.
D. ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )

A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省元.

相关试题

