搜索
【题目】 如图，小明购买一种笔记本所付款金额y（元）与购买量x（本）之间的函数图象由线段OB和射线BE组成，则一次购买8个笔记本比分8次购买每次购买1个可节省元． 
参考答案：
【答案】4
【解析】解：由线段OB的图象可知，当0＜x＜时，y=5x，
1千克苹果的价钱为：y=5，
设射线EB的解析式为y=kx+b（x≥2），
把（4，20），（10，44）代入得 
，
解得： 
，
∴射线EB的解析式为y=4x+4，
当x=8时，y=4×8+4=36，
5×8﹣36=4（元），
故答案为：4．
根据函数图象，分别求出线段OB和射线EB的函数解析式，然后可求出一次购买8个笔记本的价钱和分8次购买每次购买1个的花费，进而可得答案．本题考查了一次函数的应用，解决本题的关键是掌握待定系数法求一次函数解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分别是BG，AC的中点．
（1）求证：DE=DF，DE⊥DF；
（2）连接EF，若AC=2，求EF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 ， C1D1与AD交于点M，延长DA交A1D1于F，若AB=1，BC=
，则AF的长度为（ ）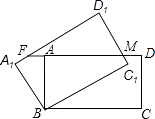 
A.2﹣
B.
C.
D. ﹣1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B、F、C、E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（ ）
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC -
科目： 来源： 题型：
查看答案和解析>>【题目】已知⊙O1和⊙O2的半径分别为m、n，且m、n满足
+（n﹣2）2=0，圆心距O1O2= 
，则两圆的位置关系为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】（操作发现）
（1）如图1，△ABC为等边三角形，先将三角板中的60°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于30°），旋转后三角板的一直角边与AB交于点D，在三角板斜边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=30°，连接AF，EF．
①求∠EAF的度数；
②DE与EF相等吗？请说明理由；
（类比探究）
（2）如图2，△ABC为等腰直角三角形，∠ACB=90°，先将三角板的90°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于45°），旋转后三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=45°，连接AF，EF．
①∠EAF= ；
②当AE=1，ED=2时，求DB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点
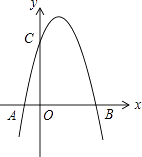
（1）求m的值及C点坐标；
（2）在直线BC上方的抛物线上是否存在一点M，使得它与B，C两点构成的三角形面积最大，若存在，求出此时M点坐标；若不存在，请简要说明理由
（3）P为抛物线上一点，它关于直线BC的对称点为Q
①当四边形PBQC为菱形时，求点P的坐标；
②点P的横坐标为t（0＜t＜4），当t为何值时，四边形PBQC的面积最大，请说明理由．
相关试题
