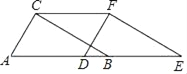
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的面积.
参考答案:
【答案】(1)3cm(2)![]()
【解析】试题分析:(1)根据勾股定理求出AB=![]() =5cm.利用平移的性质可得AB=DE=5cm,然后根据AD=AE-DE求解即可;
=5cm.利用平移的性质可得AB=DE=5cm,然后根据AD=AE-DE求解即可;
(2)作CG⊥AB于G,根据三角形的面积公式求出CG,根据梯形的面积公式求出四边形AEFC的面积即可.
试题解析:
(1)∵在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
∴AB=![]() =5cm.
=5cm.
∵△ABC沿AB方向向右平移得到△DEF,
∴AD=BE=CF,BC=EF=3cm,AB=DE=5cm.
∵AE=8cm,
∴AD=AE﹣DE=3cm;
(2)作CG⊥AB于G,如图,
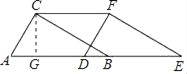
由三角形的面积公式得:CGAB=ACBC,
∴5×CG=3×4,
∴CG=![]() ,
,
∴四边形AEFC的面积=![]() (CF+AE)×CG=
(CF+AE)×CG=![]() ×(3+8)×
×(3+8)×![]() =
=![]() .
.
答:四边形AEFC的面积是![]() cm2.
cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
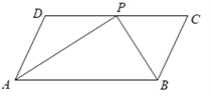
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量指数是国际上普遍采用的定量评价空气质量好坏的重要指标,空气质量指数不超过50则空气质量评估为优.下表记录了我市11月某一周7天的空气质量指数变化情况.规定:空气质量指数50记为零,空气质量指数超过50记为正,空气质量指数低于50记为负.
星期一
星期二
星期三
星期四
星期五
星期六
星期日
+18
﹣4
﹣1
﹣18
﹣10
+28
+29
解答以下问题:
(1)根据表格可知,星期四空气质量指数为 ,星期六比星期二空气质量指数高 ;
(2)求这一周7天的平均空气质量指数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组要制作长方形和梯形两种不同形状的卡片,尺寸如图所示(单位:cm).

(1)长方形卡片的面积是 cm2;若梯形卡片的下底是上底的3倍,则梯形卡片的面积是 cm2;
(2)在(1)的条件下,做5张长方形卡片比做3张梯形卡片多用料多少平方厘米?
-
科目: 来源: 题型:
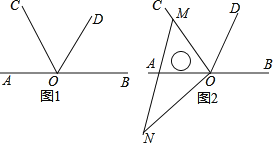
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,OD,使射线OC平分∠AOD.
(1)当∠BOD=50°时,∠COD= °;
(2)将一直角三角板的直角顶点放在点O处,当三角板MON的一边OM与射线OC重合时,如图2.
①在(1)的条件下,∠AON= °;
②若∠BOD=70°,求∠AON的度数;
③若∠BOD=α,请直接写出∠AON的度数(用含α的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E,构造出平行四边形AEDF.
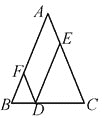
(1)若点D在线段BC上时. ①求证:FB=FD.②求证:DE+DF=AC.
(2)点D在边BC所在的直线上,若AC=8,DE=3,请作出简单示意图求DF的长度,不需要证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方方同学在寒假社会调查实践活动中,对某罐头加工厂进行采访,获得了该厂去年的部分生产信息如下:
①该厂一月份罐头加工量为a吨;
②该厂三月份的加工量比一月份增长了44%;
③该厂第一季度共加工罐头182吨;
④该厂二月、三月加工量每月按相同的百分率增长;
⑤该厂从四月份开始设备整修更新,加工量每月按相同的百分率开始下降;
⑥六月份设备整修更新完毕,此月加工量为一月份的2.1倍,与五月份相比增长了46.68吨.
利用以上信息求:
(1)该厂第一季度加工量的月平均增长率;
(2)该厂一月份的加工量a的值;
(3)该厂第二季度的总加工量.
相关试题

