【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E,构造出平行四边形AEDF.
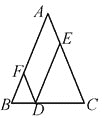
(1)若点D在线段BC上时. ①求证:FB=FD.②求证:DE+DF=AC.
(2)点D在边BC所在的直线上,若AC=8,DE=3,请作出简单示意图求DF的长度,不需要证明.
参考答案:
【答案】(1)见解析,见解析;(2)DF=BF=5或DF=BF=11 见解析.
【解析】
(1)①根据等腰三角形性质得∠B=∠C,由平行线性质得∠FDB=∠C,等量代换得∠B=∠FDB,根据等腰三角形性质:等角对等边即可得证.
②由平行四边形性质得ED=AF,AE=FD,由①知FB=FD,等量代换得AE=FB,从而可得DE+DF= AF+ FB=AB=AC.
(2)如图1:根据平行四边形性质得AF=DE=3,DF=AE,由(1)知FB=FD,由DF=BF=AB-AF=8-3=5;
如图2:根据平行四边形性质得AF=DE=3,DF=AE,由(1)知FB=FD,由DF=BF=AB+AF=8+3=11.
解:(1)①∵AB=AC,
∴∠B=∠C,
∵DF//AC,
∴∠FDB=∠C,
∴∠B=∠FDB,
∴FB=FD.
②∵四边形AEDF是平行四边形,
∴ED=AF,AE=FD,
∵FB=FD,
∴AE=FB,
∴DE+DF= AF+ FB=AB,
∵AB=AC,
∴DE+DF=AC.
(2)如图1,

∵四边形AEDF为平行四边形,
∴AF=DE,DF=AE,
由(1)知FB=FD,
∵AC=8,DE=3,AB=AC,
∴AF=3,BF=AB-AF=8-3=5,
∴DF=BF=5;
如图2,

∵四边形AEDF为平行四边形,
∴AF=DE,DF=AE,
由(1)知FB=FD,
∵AC=8,DE=3,AB=AC,
∴AF=3,BF=AB+AF=8+3=11,
∴DF=BF=11;
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组要制作长方形和梯形两种不同形状的卡片,尺寸如图所示(单位:cm).

(1)长方形卡片的面积是 cm2;若梯形卡片的下底是上底的3倍,则梯形卡片的面积是 cm2;
(2)在(1)的条件下,做5张长方形卡片比做3张梯形卡片多用料多少平方厘米?
-
科目: 来源: 题型:
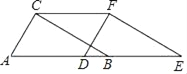
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的面积.
-
科目: 来源: 题型:
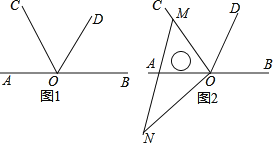
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,OD,使射线OC平分∠AOD.
(1)当∠BOD=50°时,∠COD= °;
(2)将一直角三角板的直角顶点放在点O处,当三角板MON的一边OM与射线OC重合时,如图2.
①在(1)的条件下,∠AON= °;
②若∠BOD=70°,求∠AON的度数;
③若∠BOD=α,请直接写出∠AON的度数(用含α的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】方方同学在寒假社会调查实践活动中,对某罐头加工厂进行采访,获得了该厂去年的部分生产信息如下:
①该厂一月份罐头加工量为a吨;
②该厂三月份的加工量比一月份增长了44%;
③该厂第一季度共加工罐头182吨;
④该厂二月、三月加工量每月按相同的百分率增长;
⑤该厂从四月份开始设备整修更新,加工量每月按相同的百分率开始下降;
⑥六月份设备整修更新完毕,此月加工量为一月份的2.1倍,与五月份相比增长了46.68吨.
利用以上信息求:
(1)该厂第一季度加工量的月平均增长率;
(2)该厂一月份的加工量a的值;
(3)该厂第二季度的总加工量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两个小机器人A、B在一条笔直的道路上由西向东行走,两机器人相距6cm,即AB=6cm.其中机器人A的速度为3cm/s,机器人B的速度为2cm/s.设机器人B行走的时间为t(s).
(1)若两机器人同时出发,
①当t=
 时,AB= cm;当t=7时,AB= cm;
时,AB= cm;当t=7时,AB= cm;②当两机器人相距4cm时,求机器人B行走的时间t的值;
(2)若机器人B先行走2s,机器人A再行走,当两机器人相距10cm时,请直接写出t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的表达式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式kx+b>2x-4>0的解集.
相关试题

