【题目】如图,平行四边形ABCD中,AP,BP分别平分∠DAB和∠CBA,交于DC边上点P,AD=5.
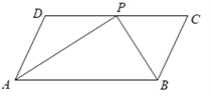
(1)求线段AB的长.
(2)若BP=6,求△ABP的周长.
参考答案:
【答案】(1)10cm;(2)24cm.
【解析】
(1)根据角平分线定义和平行线性质得∠DAP=∠BAP,∠DPA=∠PAB,等量代换得∠DAP=∠DPA,由等腰三角形性质可得DA=DP ;同理可得 CB=CP,由DC=DP+CP即可求得答案.
(2)据角平分线定义得∠BAP=![]() ∠BAD,∠PBA=
∠BAD,∠PBA=![]() ∠CBA, 由平行线性质得∠DAB+∠ABC=180°,从而可得 ∠PAB+∠PBA=90°,在Rt△APB中,根据勾股定理求得AP长,再由三角形周长即可求得答案.
∠CBA, 由平行线性质得∠DAB+∠ABC=180°,从而可得 ∠PAB+∠PBA=90°,在Rt△APB中,根据勾股定理求得AP长,再由三角形周长即可求得答案.
解:(1)在平行四边形ABCD中,
∵AP平分∠DAB,
∴∠DAP=∠BAP,
∵DC//AB,
∴∠DPA=∠PAB,
∴∠DAP=∠DPA,
∴DA=DP.
同理CB=CP,
∴AD=BC=5,
∴DC=DP+CP=10cm.
(2)∵DA//CP,
∴∠DAB+∠ABC=180° ,
∵AP平分∠DAB,BP平分∠ABC
∴∠BAP= ![]() ∠BAD,∠PBA=
∠BAD,∠PBA= ![]() ∠CBA,
∠CBA,
∴∠PAB+∠PBA=90,
∴∠APB=90,
∵AB=10,BP=6,
∴PA=8,
∴C△ABP=24cm.
-
科目: 来源: 题型:
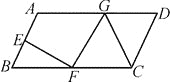
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,G是AD 上的任一点.计S1=S△BEF , S2=S△GFC ,S=S□ABCD ,则S=________S2=________S1 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某校在慈善爱心捐款活动中的统计情况,图1是各年级捐款人数占总捐款人数的百分比,图2是对部分学生捐款金额和人数的抽样调查.
(1)在抽取的样本中,捐款金额的平均数、中位数、众数各是多少?
(2)若该校九年级共有200人捐款,请你估计全校捐款的总金额约为多少元?

-
科目: 来源: 题型:
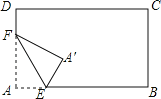
查看答案和解析>>【题目】如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,则∠FEB的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量指数是国际上普遍采用的定量评价空气质量好坏的重要指标,空气质量指数不超过50则空气质量评估为优.下表记录了我市11月某一周7天的空气质量指数变化情况.规定:空气质量指数50记为零,空气质量指数超过50记为正,空气质量指数低于50记为负.
星期一
星期二
星期三
星期四
星期五
星期六
星期日
+18
﹣4
﹣1
﹣18
﹣10
+28
+29
解答以下问题:
(1)根据表格可知,星期四空气质量指数为 ,星期六比星期二空气质量指数高 ;
(2)求这一周7天的平均空气质量指数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组要制作长方形和梯形两种不同形状的卡片,尺寸如图所示(单位:cm).

(1)长方形卡片的面积是 cm2;若梯形卡片的下底是上底的3倍,则梯形卡片的面积是 cm2;
(2)在(1)的条件下,做5张长方形卡片比做3张梯形卡片多用料多少平方厘米?
-
科目: 来源: 题型:
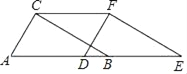
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的面积.
相关试题

