搜索
【题目】在下列条件中，△ABC不是直角三角形的是 （ ）
A. b2=a2-c2 B. ∠A：∠B：∠C=3：4：5
C. ∠C=∠A-∠B D. a2：b2：c2=1：3：2
参考答案：
【答案】B
【解析】解：A．根据勾股定理的逆定理，如果b2=a2﹣c2，那么a2=b2+c2，则△ABC为直角三角形，故本选项错误；
B．∵∠A：∠B：∠C=3：4：5，∴∠A=180°×
=45°，∠B=180°×
=60°，∠C=180°×
=75°，△ABC不是直角三角形，故本选项正确．
C．∵∠C=∠A﹣∠B，∴∠A=∠B+∠C，∴∠A=90°，△ABC是直角三角形，故本选项错误；
D．根据勾股定理的逆定理，如果a2：b2：c2=1：3：2，那么b2=a2+c2，则△ABC为直角三角形，故本选项错误；
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线的顶点为（1，-4），且经过点B（3，0）.
（Ⅰ）求该抛物线的解析式及抛物线与x轴的另一个交点A的坐标；
（Ⅱ）点P(m,t)为抛物线上的一个动点，点P关于原点的对称点为P′.
①当点P′落在该抛物线上时，求m的值；
②当点P′落在第二象限内，P′A2取得最大值时，求m的值.
-
科目： 来源： 题型：
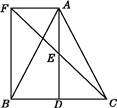
查看答案和解析>>【题目】如图，△ABC中，D是BC边上的一点，E为AD的中点，过A作BC的平行线交CE的延长线于F，且AF=BD，连接BF.
(1)求证:BD=CD;
(2)如果AB=AC，试判断四边形AFBD的形状，并证明你的结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某宾馆有50个房间共游客居住.当每个房间定价为180元时，房间会全部住满；当每个房间的定价增加10元时，就会有一个房间空闲．
设每个房间每天的定价增加x个10元.
（Ⅰ）填写下表：
每个房间每天定价（元）
180
190
200
210
……
180×10x
住满房间个数（个）
50
49
48
……
（Ⅱ）若游客居住的房间的当天收入为y(元)，写出y关于x的函数关系式；
（Ⅲ）如果游客入住房间，宾馆需对每个房间每天支出20元的各种费用．当房间定价为多少的时候，宾馆获得的利润W（元）最大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是“作已知三角形的高”的尺规作图过程.
已知：
.
求作：
边上的高
作法：如图，
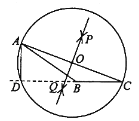
(1)分别以点
和点
为圆心，大于
的长为半径作弧，两弧相交于
， 
两点；(2)作直线
，交
于点
；(3)以
为圆心， 
为半径⊙O,与CB的延长线交于点D，连接AD，线段AD即为所作的高.请回答；该尺规作图的依据是___________________________________________________
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+2S2+2S3+S4=________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家－“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.
以
为例，花拉子米的几何解法如下：如图，在边长为
的正方形的两个相邻边上作边长分别为
和5的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形.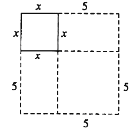
通过不同的方式来表达大正方形的面积，可以将原方程化为
）2=39+ ，从而得到此方程的正根是 .
相关试题
