【题目】已知抛物线的顶点为(1,-4),且经过点B(3,0).
(Ⅰ)求该抛物线的解析式及抛物线与x轴的另一个交点A的坐标;
(Ⅱ)点P(m,t)为抛物线上的一个动点,点P关于原点的对称点为P′.
①当点P′落在该抛物线上时,求m的值;
②当点P′落在第二象限内,P′A2取得最大值时,求m的值.
参考答案:
【答案】(Ⅰ)y=x2-2x-3,点A的坐标为(-1,0);(Ⅱ)①m1=![]() ,m2=-
,m2=-![]() . ② m=1.
. ② m=1.
【解析】试题分析: ![]() 由顶点坐标可以设抛物线的解析式为:
由顶点坐标可以设抛物线的解析式为: ![]() 把点
把点![]() 的坐标代入即可求出抛物线的解析式,进而求得抛物线与
的坐标代入即可求出抛物线的解析式,进而求得抛物线与![]() 轴的交点坐标.
轴的交点坐标.
(2)①由对称可表示出![]() 点的坐标,再由
点的坐标,再由![]() 和
和![]() 都在抛物线上,可得到关于
都在抛物线上,可得到关于![]() 的方程,可求得
的方程,可求得![]() 的值;
的值;
②由点![]() 在第二象限,可求得
在第二象限,可求得![]() 的取值范围,利用两点间距离公式可用
的取值范围,利用两点间距离公式可用![]() 表示出
表示出![]() ,再由点
,再由点![]() 在抛物线上,可用消去
在抛物线上,可用消去![]() ,整理可得到关于
,整理可得到关于![]() 的二次函数,利用二次函数的性质可求得其取得最大值时
的二次函数,利用二次函数的性质可求得其取得最大值时![]() 的值,则可求得
的值,则可求得![]() 的值.
的值.
试题解析: ![]() 设抛物线的解析式为
设抛物线的解析式为![]() 代入点
代入点![]() ,
,
![]()
![]()
∴抛物线的解析式为: ![]()
![]()
![]()
∴点![]() 的坐标为
的坐标为![]()
(Ⅱ)①由P(m,t)在抛物线上可得t=m22m3,
∵点P′与P关于原点对称,
∴P′(m,t),
∵点P′落在抛物线上,
![]() 即
即![]()
![]() 解得
解得![]() 或
或![]()
②②由题意可知P′(m,t)在第二象限,
∴m<0,t>0,即m>0,t<0,
∵抛物线的顶点坐标为(1,4),
∴4t<0,
∵P在抛物线上,
![]()
![]()
∵A(1,0),P′(m,t),
![]()
当![]() 时,
时, ![]() 取得最大值.
取得最大值.
把![]() 代入
代入![]() ,得
,得![]()
解得![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形的三个内角中,最多有_________个直角,最多有_____________个钝角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在-3≤x≤0范围内,二次函数y=ax2+bx+c(a≠0)的图像如图所示.在这个范围内,下列结论:①y有最大值1,没有最小值;②当-3<x<-1时,y随着x的增大而增大;③方程ax2+bx+c-
 =0有两个不相等的实数根.其中正确结论的个数是
=0有两个不相等的实数根.其中正确结论的个数是
A. 0个 B. 1个
C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB,∠A=50°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC的度数为( )

A. 130° B. 115° C. 110° D. 105°
-
科目: 来源: 题型:
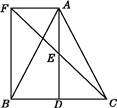
查看答案和解析>>【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间共游客居住.当每个房间定价为180元时,房间会全部住满;当每个房间的定价增加10元时,就会有一个房间空闲.
设每个房间每天的定价增加x个10元.
(Ⅰ)填写下表:
每个房间每天定价(元)
180
190
200
210
……
180×10x
住满房间个数(个)
50
49
48
……
(Ⅱ)若游客居住的房间的当天收入为y(元),写出y关于x的函数关系式;
(Ⅲ)如果游客入住房间,宾馆需对每个房间每天支出20元的各种费用.当房间定价为多少的时候,宾馆获得的利润W(元)最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,△ABC不是直角三角形的是 ( )
A. b2=a2-c2 B. ∠A:∠B:∠C=3:4:5
C. ∠C=∠A-∠B D. a2:b2:c2=1:3:2
相关试题

