搜索
【题目】古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家－“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.
以
为例，花拉子米的几何解法如下：
如图，在边长为
的正方形的两个相邻边上作边长分别为
和5的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形.
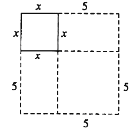
通过不同的方式来表达大正方形的面积，可以将原方程化为
）2=39+ ，从而得到此方程的正根是 .
参考答案：
【答案】5；25；3.
【解析】试题分析：通过不同的方式来表达大正方形的面积，可以将原方程化为
=
，
从而得到此方程的正根是3.
试题解析：将边长为x的正方形和边长为5的正方形，外加两个长方形，长为x，宽为5，拼合在一起面积就是x2+2x5+55，而由x2+10x35=0变形及x2+2x+25=39+25(如图所示)
即边长为x+5的正方形面积为8，所以x=3.
故答案为：5，25，3.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下列条件中，△ABC不是直角三角形的是 （ ）
A. b2=a2-c2 B. ∠A：∠B：∠C=3：4：5
C. ∠C=∠A-∠B D. a2：b2：c2=1：3：2
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是“作已知三角形的高”的尺规作图过程.
已知：
.
求作：
边上的高
作法：如图，
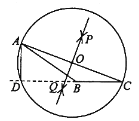
(1)分别以点
和点
为圆心，大于
的长为半径作弧，两弧相交于
， 
两点；(2)作直线
，交
于点
；(3)以
为圆心， 
为半径⊙O,与CB的延长线交于点D，连接AD，线段AD即为所作的高.请回答；该尺规作图的依据是___________________________________________________
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+2S2+2S3+S4=________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，若∠A=50°，∠B=55°，则△ABC是____________三角形；若∠A=50°，∠B=25°，则△ABC是____________三角形．（填“锐角”，“直角”或“钝角”）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系
中，点
的坐标为（1,0），点
的横坐标为2，将点 
绕点P旋转，使它的对应点
恰好落在
轴上（不与
点重合）；再将点
绕点O逆时针旋转90°得到点
.(1)直接写出点
和点C的坐标；(2)求经过A，B,C三点的抛物线的表达式.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在离水面高度为5m的岸上有人用绳子拉船靠岸，开始绳子与水面的夹角为30°，此人以每秒0.5m的速度收绳．
（1）8秒后船向岸边移动了多少米？
（2）写出还没收的绳子的长度S米与收绳时间t秒的函数关系式．
相关试题
