【题目】如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )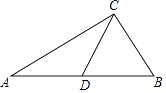
A.![]()
B.2
C.4 ![]() ﹣4
﹣4
D.![]()
参考答案:
【答案】D
【解析】∵△ACD是以AC为底的等腰三角形,
∴AD=CD,
∵△BCD与△BAC相似,
∴ ![]() =
= ![]() ,
,
设CD=x,BD=y,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() ,
,
解得:x=2y,
∴y= ![]() ,
,
∴x= ![]() ,
,
∴CD= ![]() ,
,
所以答案是:D.
【考点精析】本题主要考查了等腰三角形的性质和相似三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
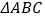 中,BC的垂直平分线EF交
中,BC的垂直平分线EF交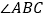 的平分线BD于点E,若
的平分线BD于点E,若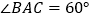 ,
, ,那么
,那么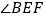 的大小是( )
的大小是( )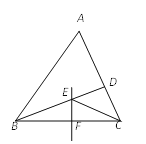
A.
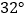 B.
B. 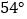 C.
C. 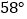 D.
D. 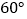
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=
 x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离
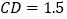 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
A. 2米B. 2.5米C. 2.25米D. 3米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,BC=10cm,点P、点Q同时从点B出发,点P以2cm/s的速度沿B→A→C运动,终点为C,点Q以1cm/s的速度沿B→C运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,△BPQ的面积为ycm2 , 已知y与t的函数关系的图象如图2(曲线OM和MN均为抛物线的一部分),给出以下结论:①AC=6cm;②曲线MN的解析式为y=﹣
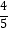 t2+
t2+ 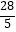 t(4≤t≤7);③线段PQ的长度的最大值为
t(4≤t≤7);③线段PQ的长度的最大值为 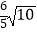 ;④若△PQC与△ABC相似,则t=
;④若△PQC与△ABC相似,则t= 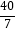 秒.其中正确的是( )
秒.其中正确的是( )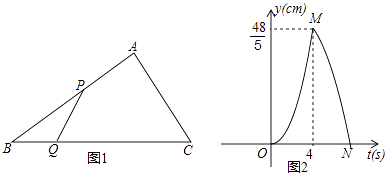
A.①②④
B.②③④
C.①③④
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作EFGD,连结BG,分别交EF和DC于点M,N,则
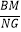 = .
= . 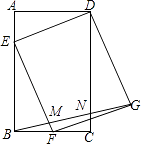
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,同底数幂的乘法法则为:am·an=am+n(其中a≠0,m,n为正整数),类似地我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=
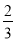 ,则h(2)=________;
,则h(2)=________;(2)若h(1)=k(k≠0),则h(n)·h(2017)=________(用含n和k的代数式表示,其中n为正整数).
相关试题

