【题目】我们知道,同底数幂的乘法法则为:am·an=am+n(其中a≠0,m,n为正整数),类似地我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=![]() ,则h(2)=________;
,则h(2)=________;
(2)若h(1)=k(k≠0),则h(n)·h(2017)=________(用含n和k的代数式表示,其中n为正整数).
参考答案:
【答案】 ![]() kn+2017
kn+2017
【解析】(1)∵h(1)=![]() ,∴h(2)=h(1)·h(1)=
,∴h(2)=h(1)·h(1)=![]() ×
×![]() =
=![]() .
.
(2)∵h(1)=k,∴h(2)=h(1)·h(1)=k2,
∴h(3)=h(1)·h(2)=k3,
同理可得h(4)=k4,h(5)=k5……∴h(n)=kn.
∴h(n)·h(2017)=h(n+2017)=kn+2017.
故答案为:(1)![]() ;(2)kn+2017.
;(2)kn+2017.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与探究.
(1)分别画出图①中“
 ”和“
”和“ ”关于直线l的对称图形(画出示意图即可).
”关于直线l的对称图形(画出示意图即可).(2)图②中小冬和小亮上衣上印的字母分别是什么?
(3)把字母“
 ”和“
”和“ ”写在薄纸上,观察纸的背面,写出你看到的字母背影.
”写在薄纸上,观察纸的背面,写出你看到的字母背影.(4)小明站在五个学生的身后,这五个学生正向前方某人用手势示意一个五位数,从小明站的地方看(如图③所示),这个五位数是23456.请你判断出他们示意的真实五位数是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB =AC=2,∠B = 40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE = 40°,DE交线段AC于点E.
(1)当∠BDA = 115°时,∠BAD= °,∠DEC = °,当点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”) .
(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:
(1).填空:请用文字语言叙述勾股定理的逆定理:__________.
勾股定理的逆定理所给出的判定一个三角形是直角三角形的方法,和学过的一些其它几何图形的判定方法不同,它通过计算来判断.实际上计算在几何中也是很重要的,从数学方法这个意义上讲,我们学习勾股定理的逆定理,更重要的是拓展思维,进一步体会数学中的各种方法.
(2).阅读:小明在学习勾股定理后,尝试着利用计算的方法进行论证,解决了如下问题:
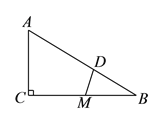
如图
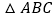 中,
中,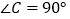 ,
, 是
是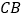 的中点,
的中点,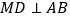 于
于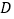 ,请说明三条线段
,请说明三条线段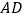 、
、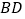 、
、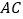 总能构成一个直角三角形.
总能构成一个直角三角形.证明:设
 ,
,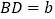 ,
,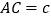 ,
,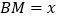 ,
,∵
 是
是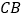 的中点,∴
的中点,∴ ,
,在
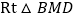 中,
中, ,
,在
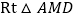 中,
中,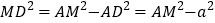 ,
,消去
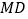 ,得
,得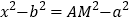 ,从而,
,从而,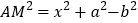 ,
,又因为在
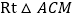 中,
中,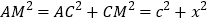 ,
,消去
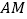 得
得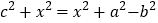 ,消去
,消去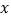 ,所以
,所以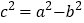 ,即
,即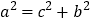 .
.所以,三条线段
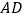 、
、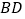 、
、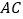 总能构成一个直角三角形.
总能构成一个直角三角形.可见,计算在几何证明中也是很重要的.小明正是利用代数中计算、消元等手段,结合相关定理来论证了几何问题.
(3).解决问题:在矩形
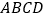 中,点
中,点 、
、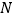 、
、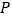 、
、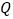 分别在边
分别在边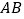 、
、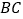 、
、 、
、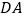 上,使得
上,使得 ,求证:四边形
,求证:四边形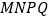 是平行四边形.
是平行四边形.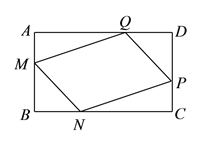
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.

(1)∠ECD和∠EDC相等吗?说明理由.
(2)OC和OD相等吗?说明理由.
(3)OE是线段CD的垂直平分线吗?说明理由.
相关试题

