【题目】如图1,在Rt△ABC中,∠A=90°,BC=10cm,点P、点Q同时从点B出发,点P以2cm/s的速度沿B→A→C运动,终点为C,点Q以1cm/s的速度沿B→C运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,△BPQ的面积为ycm2 , 已知y与t的函数关系的图象如图2(曲线OM和MN均为抛物线的一部分),给出以下结论:①AC=6cm;②曲线MN的解析式为y=﹣ ![]() t2+
t2+ ![]() t(4≤t≤7);③线段PQ的长度的最大值为
t(4≤t≤7);③线段PQ的长度的最大值为 ![]() ;④若△PQC与△ABC相似,则t=
;④若△PQC与△ABC相似,则t= ![]() 秒.其中正确的是( )
秒.其中正确的是( )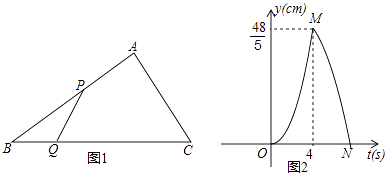
A.①②④
B.②③④
C.①③④
D.①②③
参考答案:
【答案】A
【解析】由图2可得到t=4时,y= 48 5 ,
∴AB=2×4=8cm,
∵∠A=90°,BC=10cm,
∴AC=6cm,
故①正确;
②当P在AC上时,如图3,过P作PD⊥BC于D,
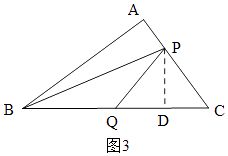
此时: ![]() =7,
=7,
∴4≤t≤7,
由题意得:AB+AP=2t,BQ=t,
∴PC=14﹣2t,
sin∠C= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PD= ![]() ,
,
∴y=S△BPQ= ![]() BQPD=
BQPD= ![]() t
t ![]() =﹣
=﹣ ![]() ;
;
故②正确;
③当P与A重合时,PQ最大,如图4,此时t=4,
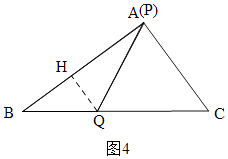
∴BQ=4,
过Q作GH⊥AB于H,
sin∠ ![]() ,
,
∴ ![]() ,
,
∴QH= ![]() ,
,
同理:BH= ![]() ,
,
∴AH=8﹣ ![]() =
= ![]() ,
,
∴PQ= ![]() =
= ![]() =
= ![]() ;
;
∴线段PQ的长度的最大值为 ![]() ;
;
故③不正确;
④若△PQC与△ABC相似,点P只有在线段AC上,
分两种情况:
PC=14﹣2t,QC=10﹣t,
i)当△CPQ∽△CBA,如图5,则 ![]() ,
,
∴ ![]() ,
,
解得t=﹣8不合题意.
ii)当△PQC∽△BAC时,如图5,
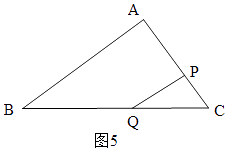
∴ ![]() ,
,
∴ ![]() ,
,
t= ![]() ;
;
∴若△PQC与△ABC相似,则t= ![]() 秒,
秒,
故④正确;
其中正确的有:①②④.
所以答案是:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=
 x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离
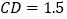 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
A. 2米B. 2.5米C. 2.25米D. 3米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
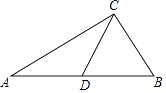
A.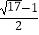
B.2
C.4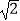 ﹣4
﹣4
D.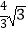
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作EFGD,连结BG,分别交EF和DC于点M,N,则
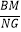 = .
= . 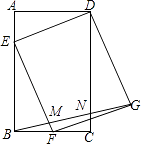
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,同底数幂的乘法法则为:am·an=am+n(其中a≠0,m,n为正整数),类似地我们规定关于任意正整数m,n的一种新运算:h(m+n)=h(m)·h(n),请根据这种新运算填空:
(1)若h(1)=
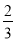 ,则h(2)=________;
,则h(2)=________;(2)若h(1)=k(k≠0),则h(n)·h(2017)=________(用含n和k的代数式表示,其中n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,点D,E,F分别在BC,AB,AC边上.
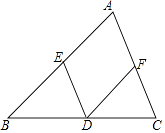
(1)当点D,E,F分别为BC,AB,AC边的中点时,求证:△BED≌△DFC;
(2)若DE∥AC,DF∥AB,且AE=2,BE=3,求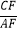 的值.
的值.
相关试题

