【题目】如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y= ![]() x刻画.
x刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
参考答案:
【答案】
(1)解:由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4)
(2)解:联立两解析式可得: 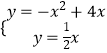 ,
,
解得: ![]() ,或
,或 ![]() .
.
故可得点A的坐标为( ![]() ,
, ![]() )
)
(3)解:如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
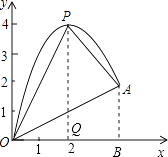
S△POA=S△POQ+S梯形PQBA﹣S△BOA
= ![]() ×2×4+
×2×4+ ![]() ×(
×( ![]() +4)×(
+4)×( ![]() ﹣2)﹣
﹣2)﹣ ![]() ×
× ![]() ×
× ![]()
=4+ ![]() ﹣
﹣ ![]()
= ![]()
(4)解:过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
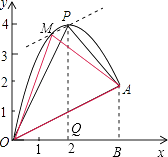
设直线PM的解析式为y= ![]() x+b,
x+b,
∵P的坐标为(2,4),
∴4= ![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直线PM的解析式为y= ![]() x+3.
x+3.
由 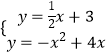 ,解得
,解得 ![]() ,
, 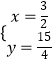 ,
,
∴点M的坐标为( ![]() ,
, ![]() ).
).
【解析】(1)利用配方法可配成顶点式;(2)A点的坐标可通过求抛物线与直线解析式联立的方程组的解即可;(3)“斜三角形”面积可通过作垂线转化为“竖直三角形”的面积和;(4)底边公用的三角形面积相等可逆向思维,可由“平行线所夹的底边共用三角形面积相等”得到直线PM![]() OA,求出PM解析式与抛物线的交点,即可求出M坐标.
OA,求出PM解析式与抛物线的交点,即可求出M坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)12016 +
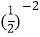 3.14 π 0
3.14 π 0 (2) 3a2 3 2a a5
(3) x 2 x 1 3xx 1
(4)2a b c2a b c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A、B、C在坐标轴上,且A、B、C的坐标分别为
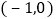 、
、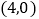 、
、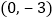 过点A的直线AD与y轴正半轴交于点D,
过点A的直线AD与y轴正半轴交于点D,
 求直线AD和BC的解析式;
求直线AD和BC的解析式;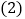 如图2,点E在直线
如图2,点E在直线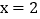 上且在直线BC上方,当
上且在直线BC上方,当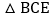 的面积为6时,求E点坐标;
的面积为6时,求E点坐标;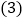 在
在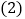 的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当
的条件下,如图3,动点M在直线AD上,动点N在x轴上,连接ME、NE、MN,当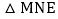 周长最小时,求
周长最小时,求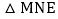 周长的最小值.
周长的最小值.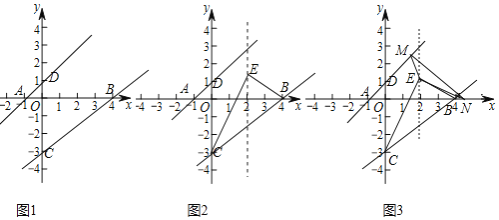
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
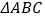 中,BC的垂直平分线EF交
中,BC的垂直平分线EF交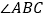 的平分线BD于点E,若
的平分线BD于点E,若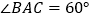 ,
, ,那么
,那么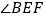 的大小是( )
的大小是( )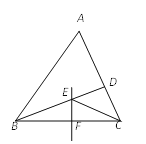
A.
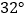 B.
B. 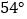 C.
C. 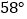 D.
D. 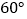
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离
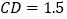 米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
米。竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
A. 2米B. 2.5米C. 2.25米D. 3米
-
科目: 来源: 题型:
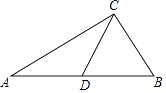
查看答案和解析>>【题目】如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
A.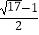
B.2
C.4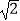 ﹣4
﹣4
D.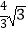
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,BC=10cm,点P、点Q同时从点B出发,点P以2cm/s的速度沿B→A→C运动,终点为C,点Q以1cm/s的速度沿B→C运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,△BPQ的面积为ycm2 , 已知y与t的函数关系的图象如图2(曲线OM和MN均为抛物线的一部分),给出以下结论:①AC=6cm;②曲线MN的解析式为y=﹣
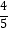 t2+
t2+ 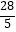 t(4≤t≤7);③线段PQ的长度的最大值为
t(4≤t≤7);③线段PQ的长度的最大值为 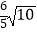 ;④若△PQC与△ABC相似,则t=
;④若△PQC与△ABC相似,则t= 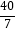 秒.其中正确的是( )
秒.其中正确的是( )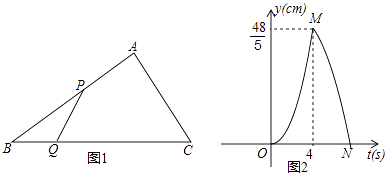
A.①②④
B.②③④
C.①③④
D.①②③
相关试题

