【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

参考答案:
【答案】![]() .
.
【解析】试题分析:根据矩形的性质就可以得出EF,AP互相平分,且EF=AP,根据垂线段最短的性质就可以得出AP⊥BC时,AP的值最小,即AM的值最小,由勾股定理求出BC,根据面积关系建立等式求出其解即可.
∵PE⊥AB,PF⊥AC,∠BAC=90°,∴∠EAF=∠AEP=∠AFP=90°,∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP, ∴EF,AP的交点就是M点, ∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小. ∵AP×BC=AB×AC, ∴AP×BC=AB×AC,
在Rt△ABC中,由勾股定理,得BC=![]() =10, ∵AB=6,AC=8, ∴10AP=6×8, ∴AP=
=10, ∵AB=6,AC=8, ∴10AP=6×8, ∴AP=![]()
∴AM=![]() ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)5.6+(﹣0.9)+4.4+(﹣8.1)+(﹣0.1)
(2)5+(﹣
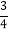 )﹣7﹣(﹣2.5)
)﹣7﹣(﹣2.5)(3)(﹣
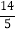 )×(﹣
)×(﹣ )+(﹣
)+(﹣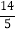 )×(+
)×(+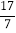 )
)(4)
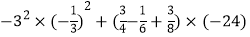
(5)8﹣23÷(﹣4)3+

(6)(﹣1)2018+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=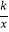 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b>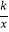 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.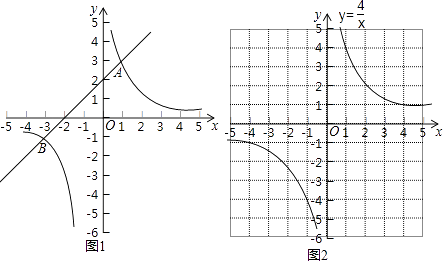
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=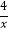 ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=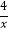 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标,观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集 -
科目: 来源: 题型:
查看答案和解析>>【题目】某仓库本周运进货物件数和运出货物件数如下表:
星期
一
二
三
四
五
六
日
运进货物件数
5
a
5
5
b
5
5
运出货物件数
12
2a
8
0
b﹣5
5
10
(1)如果用正数表示运进货物件数,负数表示运出货物件数,请你分别表示出周二、周五当天进出货物后变化的量;
(2)若经过一周的时间,仓库货物总量相比上周末库存量减少了5件,求a的值;
(3)若本周运进货物总件数比运出货物件数的一半多15件,本周运进货物总件数比上周减少
 ,而本周运出货物总件数比上周多
,而本周运出货物总件数比上周多 ,这两周内,该仓库货物共增加了3件,求a、b的值.
,这两周内,该仓库货物共增加了3件,求a、b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

-
科目: 来源: 题型:
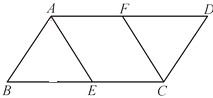
查看答案和解析>>【题目】如图,在ABCD中,BC=2AB=4,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
相关试题

