搜索
【题目】计算
（1）5.6+（﹣0.9）+4.4+（﹣8.1）+（﹣0.1）
（2）5+（﹣
）﹣7﹣（﹣2.5）
（3）（﹣
）×（﹣
）+（﹣）×（+
）
（4）
（5）8﹣23÷（﹣4）3+
（6）（﹣1）2018+（﹣5）×[（﹣2）3+2]﹣（﹣4）2÷（﹣
）
参考答案：
【答案】（1）0.9；（2）﹣0.25；（3）﹣6；（4）﹣24；（5）8
；（6）63．
【解析】
（1）利用加法结合律，进行加减运算即可求解；
（2）把减法转化为加法，根据法则进行运算即可.
（3）首先计算乘法，最后进行加减运算即可求解；
（4）首先计算乘方，再利用分配律计算即可；
（5）首先计算乘方，计算括号内的式子，再计算除法，最后进行加减运算即可；
（6）首先计算乘方，计算括号内的式子，再计算除法，最后进行加减运算即可；
（1）原式=（5.6+4.4）+（﹣0.9﹣8.1﹣0.1）
=10﹣9.1
=0.9；
（2）原式=5﹣0.75﹣7+2.5
=7.5﹣7.75
=﹣0.25；
（3）原式
（4）原式
=﹣1﹣18+4﹣9，
=﹣24；
（5）原式
（6）原式=1+（﹣5）×（﹣8+2）﹣16×（﹣2）
=1+（﹣5）×（﹣6）+32
=1+30+32
=63．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，为美化校园环境，某校计划在一块长为100米，宽为60米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为a米﹒
（1）用含a的式子表示花圃的面积；
（2）如果通道所占面积是整个长方形空地面积的
，求出此时通道的宽；（3）已知某园林公司修建通道的单价是50元/米2，修建花圃的造价y（元）与花圃的修建面积S（m2）之间的函数关系如图2所示，并且通道宽a（米）的值能使关于x的方程
x2-ax+25a-150有两个相等的实根，并要求修建的通道的宽度不少于5米且不超过12米，如果学校决定由该公司承建此项目，请求出修建的通道和花圃的造价和为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是_____（填写符合要求的序号）
（1）两个有理数的和为负数时，这两个数都是负数；
（2）如果两个数的差是正数，那么这两个数都是正数；
（3）几个有理数相乘，当负因数个数为奇数时，乘积一定为负；
（4）数轴上到原点的距离为3的点表示的数是3或﹣3；
（5）0乘以任何数都是0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为
A．
B．3 C．1 D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2=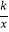
交于A（1，3）和B（﹣3，﹣1）两点．
观察图象可知：
①当x=﹣3或1时，y1=y2；
②当﹣3＜x＜0或x＞1时，y1＞y2 ， 即通过观察函数的图象，可以得到不等式ax+b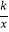＞ 的解集．
有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．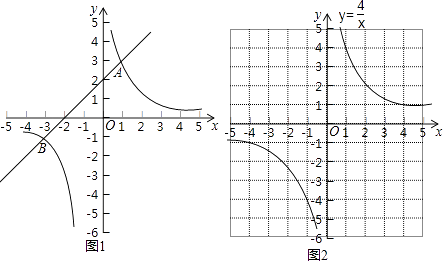
下面是他的探究过程，请将（2）、（3）、（4）补充完整：
（1）将不等式按条件进行转化：
（2）构造函数，画出图象
设y3=x2+4x﹣1，y4=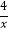
，在同一坐标系中分别画出这两个函数的图象．
双曲线y4=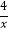 如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）
（3）确定两个函数图象公共点的横坐标，观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为
（4）借助图象，写出解集
结合（1）的讨论结果，观察两个函数的图象可知：不等式x3+4x2﹣x﹣4＞0的解集 -
科目： 来源： 题型：
查看答案和解析>>【题目】某仓库本周运进货物件数和运出货物件数如下表：
星期
一
二
三
四
五
六
日
运进货物件数
5
a
5
5
b
5
5
运出货物件数
12
2a
8
0
b﹣5
5
10
（1）如果用正数表示运进货物件数，负数表示运出货物件数，请你分别表示出周二、周五当天进出货物后变化的量；
（2）若经过一周的时间，仓库货物总量相比上周末库存量减少了5件，求a的值；
（3）若本周运进货物总件数比运出货物件数的一半多15件，本周运进货物总件数比上周减少
，而本周运出货物总件数比上周多
，这两周内，该仓库货物共增加了3件，求a、b的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是 ．
相关试题
