【题目】某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.
(1)若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
参考答案:
【答案】
(1)解:设购买茶花树苗x株,桂花树苗y株,依题可得:
![]() ,
,
解得 ![]() .
.
答:购买茶花树苗400株,桂花树苗200株.
(2)解:设购买茶花树苗z株,桂花树苗(600﹣z)株,依题可得:
80%z+90%(600﹣z)≥85%×600,
解得z≤300.
答:茶花树苗至多购买300株.
(3)解:设买茶花树苗购买m株,购买树苗的费用为W元,依题可得:
W=35m+40(600﹣m)=﹣5m+24000
∵﹣5<0,
∴W随m的增大而减小,
∵0<m≤300,
∴当m=300时,W有最小值.W=24000﹣5×300=22500元.
答:当选购买茶花树苗300株,桂花树苗300株时,总费用最低为22500元.
【解析】(1)设购买茶花树苗x株,桂花树苗y株,根据题意可得一个二元一次方程组,解之即可得出答案.
(2)设购买茶花树苗z株,桂花树苗(600﹣z)株,根据题意可得一元一次不等式方程,解之即可得出答案.
(3)设买茶花树苗购买m株,购买树苗的费用为W元,根据题意可得W=35m+40(600﹣m)=﹣5m+24000,再根据一次函数的性质﹣5<0,W随m的增大而减小,由自变量的取值范围:0<m≤300,得出Wmin.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋,立即通知在B处的另一艘军舰一起向其包抄,此时B在A的南偏西30°方向,我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向,已知A,B之间的距离是30海里,求此刻我两艘军舰所在地A,B与C的距离.(结果保留根号)
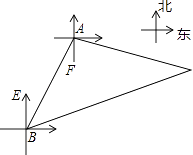
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
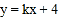 的图象经过点(-3,-2).
的图象经过点(-3,-2).(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是长方形纸袋,将纸袋沿EF折叠成图2,再沿BF折叠成图3,若∠DEF=α,用α表示图3中∠CFE的大小为 _________ .
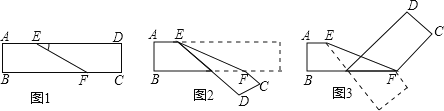
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整.
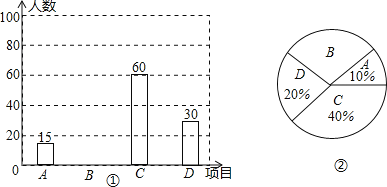
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级为了开展球类兴趣小组,需要购买一批足球和篮球﹒若购买3个足球和5个篮球需580元;若购买4个足球和3个篮球需480元.
(1)求出足球和篮球的的单价分别是多少?
(2)已知该年级决定用800元购进这两种球,若两种球都要有,请问有几种购买方案,并请加以说明﹒
相关试题

