【题目】一次函数![]() 的图象经过点(-3,-2).
的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
参考答案:
【答案】(1)y=2x+4;(2)不在;(3)(3,10)或(-3,-2)
【解析】
(1)把已知点的坐标代入y=kx+4,则可得到k的一次方程,然后解方程求出k即可得到函数解析式;
(2)根据一次函数图象上点的坐标特征进行判断;
(3)利用点M到y轴的距离是3得到M点的横坐标为3或-3,然后计算对应的函数值即可得到M点坐标.
解:(1)把(-3,-2)代入y=kz+b得-3k+4=-2,解得k=2,
所以函数解析式为y=2x+4;
(2)当x=-5时,y=2x+4=2![]() (-5)+4=-6,
(-5)+4=-6,
所以点(-5,3)不在这个函数的图象上;
(3)当x=3时,y=2x+4=10,此时M点坐标为(3,10);
当x=-3时,y=2x+4=-2,此时M点坐标为(-3,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
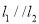 ,直线
,直线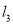 与直线
与直线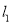 、
、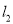 分别相交于C、D两点.
分别相交于C、D两点.(1)如图a,有一动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中,是否始终具有∠3+∠1=∠2这一关系,为什么?
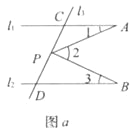
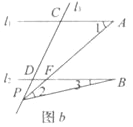
(2)如图b,当动点P线段CD之外运动(不与C、D两点重合),问上述结论是否成立?若不成立,试写出新的结论并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.

-
科目: 来源: 题型:
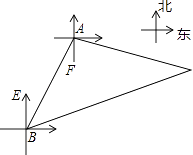
查看答案和解析>>【题目】如图,我东海舰队的一艘军舰在海面A处巡逻时发现一艘不明国籍的船只在C处游弋,立即通知在B处的另一艘军舰一起向其包抄,此时B在A的南偏西30°方向,我两艘军舰分别测得C在A的南偏东75°方向和C在B的北偏东75°方向,已知A,B之间的距离是30海里,求此刻我两艘军舰所在地A,B与C的距离.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.
(1)若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用. -
科目: 来源: 题型:
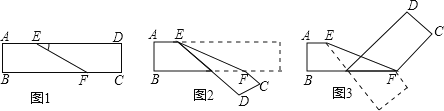
查看答案和解析>>【题目】如图1是长方形纸袋,将纸袋沿EF折叠成图2,再沿BF折叠成图3,若∠DEF=α,用α表示图3中∠CFE的大小为 _________ .
相关试题

