【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
参考答案:
【答案】(1)每张门票的原定票价为400元;(2)平均每次降价10%.
【解析】试题分析:(1)设每张门票的原定票价为x元,则现在每张门票的票价为(x-80)元,根据“按原定票价需花费6000元购买的门票张数,现在只花费了4800元”建立方程,解方程即可;
(2)设平均每次降价的百分率为y,根据“原定票价经过连续二次降价后降为324元”建立方程,解方程即可.
试题解析:(1)设每张门票的原定票价为x元,则现在每张门票的票价为(x-80)元,根据题意得
![]() ,
,
解得x=400.
经检验,x=400是原方程的根.
答:每张门票的原定票价为400元;
(2)设平均每次降价的百分率为y,根据题意得
400(1-y)2=324,
解得:y1=0.1,y2=1.9(不合题意,舍去).
答:平均每次降价10%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
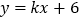 与
与 轴
轴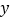 轴分别交于点
轴分别交于点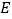 、
、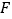 ,点
,点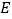 的坐标为
的坐标为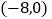 ,点
,点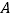 的坐标为
的坐标为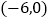 .
.(
 )求
)求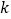 的值.
的值.(
 )若点
)若点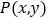 是第二象限内的直线
是第二象限内的直线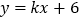 上的一个动点,在点
上的一个动点,在点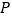 的运动过程中,试写出
的运动过程中,试写出 的面积
的面积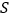 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围.
的取值范围.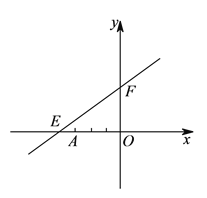
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验与探究:
(
 )由图观察易知
)由图观察易知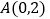 关于直线
关于直线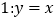 的对称点
的对称点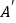 的坐标为
的坐标为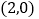 ,请在图中分别标明
,请在图中分别标明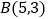 、
、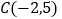 关于直线
关于直线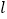 的对称点
的对称点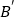 、
、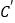 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: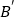 __________、
__________、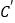 __________.
__________.归纳与发现:
(
 )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点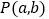 关于第一、三象限的角平分线
关于第一、三象限的角平分线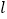 的对称点
的对称点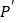 的坐标为__________(不必证明).
的坐标为__________(不必证明).运用与拓广:
(
 )已知两点
)已知两点 、
、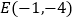 ,试在直线
,试在直线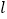 上确定一点
上确定一点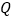 ,使点
,使点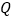 到
到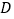 、
、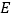 两点的距离之和最小,并求出
两点的距离之和最小,并求出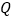 点坐标.
点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知长方形
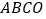 ,
,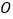 为坐标原点,
为坐标原点,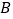 点坐标为
点坐标为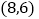 ,
,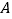 点在
点在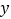 轴的正半轴上,
轴的正半轴上,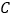 点在
点在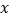 轴的正半轴上,
轴的正半轴上,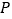 是线段
是线段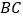 上的动点,设
上的动点,设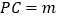 ,已知点
,已知点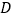 在第一象限且是直线
在第一象限且是直线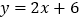 上一点,若
上一点,若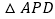 是等腰直角三角形.
是等腰直角三角形.(
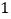 )求点
)求点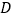 的坐标并写出解题过程.
的坐标并写出解题过程.(
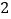 )直角
)直角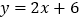 向下平移
向下平移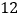 个单位后,在该直线上是否存在点
个单位后,在该直线上是否存在点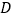 ,使
,使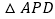 是等腰直角三角形.
是等腰直角三角形.
相关试题

