【题目】己知长方形![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 点坐标为
点坐标为![]() ,
,![]() 点在
点在![]() 轴的正半轴上,
轴的正半轴上,![]() 点在
点在![]() 轴的正半轴上,
轴的正半轴上,![]() 是线段
是线段![]() 上的动点,设
上的动点,设![]() ,已知点
,已知点![]() 在第一象限且是直线
在第一象限且是直线![]() 上一点,若
上一点,若![]() 是等腰直角三角形.
是等腰直角三角形.
(![]() )求点
)求点![]() 的坐标并写出解题过程.
的坐标并写出解题过程.
(![]() )直角
)直角![]() 向下平移
向下平移![]() 个单位后,在该直线上是否存在点
个单位后,在该直线上是否存在点![]() ,使
,使![]() 是等腰直角三角形.
是等腰直角三角形.

参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )存在点
)存在点![]() ,使
,使![]() 为等腰直角三角形,
为等腰直角三角形,![]() 坐标为
坐标为![]() ,
,![]() ,
,![]() .
.
【解析】试题分析:
(1)由点D和点A都在直线y=2x+6上可知,若△APD是等腰直角三角形,则只能是点A为直角顶点,如图,过点D作DE⊥y轴于点E,则易证![]() ≌
≌![]() ,由此可得
,由此可得![]() ,
,![]() ,从而可得点D的坐标为(6-m,14),将D的坐标代入y=2x+6中,解得m的值,即可得到点D的坐标;
,从而可得点D的坐标为(6-m,14),将D的坐标代入y=2x+6中,解得m的值,即可得到点D的坐标;
(2)将直线y=2x+6向下平移12个单位所得新直线的解析式为:y=2x-6,由图可知,点A、P在直线y=2x-6两侧,故当△APD为等腰直角三角形时,存在∠ADP=90°,∠APD=90°两种可能情况,其中当∠ADP=90°时,又存在点D在点A的上方和下方两种情况,如图2、图3和图4,然后结合已知条件进行推理计算即可.
试题解析:
(![]() )∵点A、D都在直线y-2x+6上,
)∵点A、D都在直线y-2x+6上,
∴当△APD是等腰直角三角形时,只能是点A为直角顶点,
如图1:过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
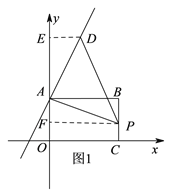
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
代入![]() 中得:-2m+6=14,解得:m=2,
中得:-2m+6=14,解得:m=2,
∴![]() ;
;
(![]() )存在点
)存在点![]() ,使
,使![]() 为等腰直角三角形,
为等腰直角三角形,
直线![]() 向下平移
向下平移![]() 个单位后变成
个单位后变成![]() ,
,
当![]() 时,
时,
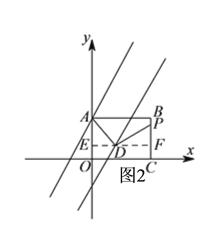
①、如图2所示,过![]() 作
作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]() .
.
∴![]() ,
,
代入![]() 中得,
中得,
![]() ,
,
∴![]() .
.
②如图3所示:
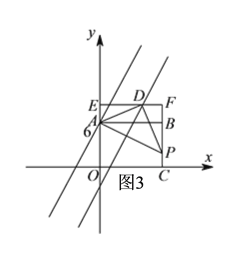
过![]() 作
作![]() 平行线
平行线![]() 交
交![]() 延长线于
延长线于![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() 中得,
中得,
![]() ,
,
∴![]() .
.
③当![]() 时,如图4,过
时,如图4,过![]() 作
作![]() ,交其垂线
,交其垂线![]() 于
于![]() ,
,
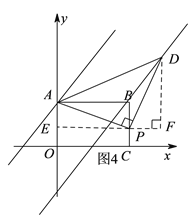
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() 中,
中,
![]() ,
,
∴![]() ,
,
综上所述,点D的坐标为![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验与探究:
(
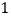 )由图观察易知
)由图观察易知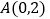 关于直线
关于直线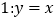 的对称点
的对称点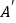 的坐标为
的坐标为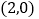 ,请在图中分别标明
,请在图中分别标明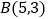 、
、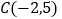 关于直线
关于直线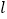 的对称点
的对称点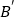 、
、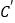 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: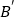 __________、
__________、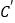 __________.
__________.归纳与发现:
(
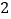 )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点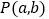 关于第一、三象限的角平分线
关于第一、三象限的角平分线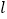 的对称点
的对称点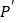 的坐标为__________(不必证明).
的坐标为__________(不必证明).运用与拓广:
(
 )已知两点
)已知两点 、
、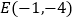 ,试在直线
,试在直线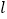 上确定一点
上确定一点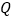 ,使点
,使点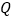 到
到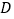 、
、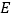 两点的距离之和最小,并求出
两点的距离之和最小,并求出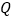 点坐标.
点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
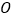 是等边
是等边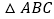 内的任一点,连接
内的任一点,连接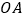 ,
, ,
,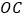 .
.如图
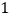 ,已知
,已知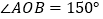 ,
,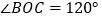 ,将
,将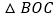 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转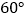 ,使
,使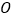 与
与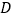 重合,得
重合,得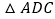 .
.(
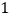 )
)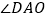 的度数是__________.
的度数是__________.(
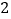 )用等式表示线段
)用等式表示线段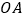 ,
, ,
,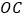 之间的数量关系,并证明.(图
之间的数量关系,并证明.(图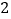 为备用图)
为备用图)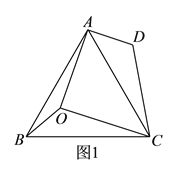
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )

A. 4月份三星手机销售额为65万元
B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
相关试题

