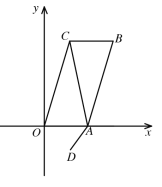
【题目】如图,在平面直角坐标系xOy中,O为原点,点A、C 的坐标分别为(2,0)、(1,3![]() ),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-
),将△AOC绕AC的中点旋转180°,点O落到点B的位置,D的坐标为(1,-![]() ).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
).若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,则点P的坐标为_________.
参考答案:
【答案】(-1,0)或(1,0)或(3,0)
【解析】
设P点坐标为(a,0),另一个顶点为Q,坐标为(0,b),分三种情况讨论,根据平行四边形对角线互相平分,则两条对角线的中点相同,利用中点坐标公式建立方程求出a即可得到P点坐标.
设P点坐标为(a,0),另一个顶点为Q,坐标为(0,b),分三种情况讨论:
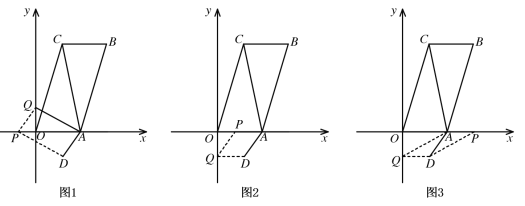
①如图1,当AP、DQ为对角线时,
∵A(2,0),D (1,-![]() ),由平行四边形对角线互相平分的性质和中点坐标公式可得,
),由平行四边形对角线互相平分的性质和中点坐标公式可得,
![]() ,解得
,解得![]() ,
,
∴P点坐标为(-1,0)
②如图2,当AQ、PD为对角线时,
同理可得![]() ,解得
,解得![]()
∴P点坐标为(1,0)
③如图3,当AD、PQ为对角线时,
同理可得![]() ,解得
,解得![]()
∴P点坐标为(3,0)
综上可得P点坐标为(-1,0)或(1,0)或(3,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形 ABCD 中,两条邻边长分别为3和5,∠BAD与∠ABC的平分线交于点E,点F 是CD的中点,连接EF,则EF=________.
-
科目: 来源: 题型:
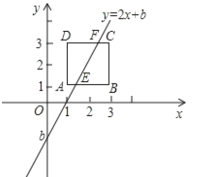
查看答案和解析>>【题目】如图,已知正方形ABCD的顶点A(1,1),B(3,1),直线y=2x+b交边AB于点E,交边CD于点F,则直线y=2x+b 在y 轴上的截距b的变化范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数







进球次数








进球频率

________
________
________
________
________
________
________
 将上表补充完整;
将上表补充完整; 这位运动员投篮一次,进球的概率约是多少?
这位运动员投篮一次,进球的概率约是多少? 若这位运动员投篮
若这位运动员投篮 次,必定会投进
次,必定会投进 次吗?为什么?
次吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线 l 经过点A(2,﹣3),与 x 轴交于点 B,且与直线y=3x-
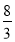 平行.
平行.(1)求直线l的函数解析式及点B的坐标;
(2)如直线l上有一点 M(a,﹣6),过点 M 作 x 轴的垂线,交直线 y=3x-
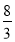 于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.
于点N,在线段MN上求一点P,使△PAB是直角三角形,请求出点P的坐标.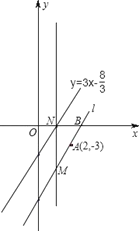
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

相关试题

