Question

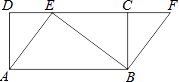
【题目】如图，等腰三角形中，，分别是两腰上的中线．

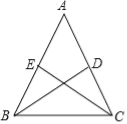
（1）求证：；

（2）设与相交于点，点，分别为线段和的中点．当的重心到顶点的距离与底边长相等时，判断四边形的形状，无需说明理由．

Answer 1

【答案】（1）证明见解析；（2）四边形DEMN是正方形.

【解析】

试题分析：（1）根据已知条件得到AD=AE，根据全等三角形的性质即可得到结论；

（2）根据三角形中位线的性质得到ED∥BC，ED=BC，MN∥BC，MN=BC，等量代换得到ED∥MN，ED=MN，推出四边形EDNM是平行四边形，由（1）知BD=CE，求得DM=EN，得到四边形EDNM是矩形，根据全等三角形的性质得到OB=OC，由三角形的重心的性质得到O到BC的距离=BC，根据直角三角形的判定得到BD⊥CE，于是得到结论．

试题解析：（1）由题意得，AB=AC，

∵BD，CE分别是两腰上的中线，∴AD=AC，AE=AB，∴AD=AE，

在△ABD和△ACE中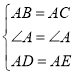 ，∴△ABD≌△ACE（ASA）．∴BD=CE；

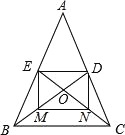
（2）四边形DEMN是正方形，

理由：∵E、D分别是AB、AC的中点，∴AE=AB，AD=AC，ED是△ABC的中位线，∴ED∥BC，ED=BC，

∵点M、N分别为线段BO和CO中点，∴OM=BM，ON=CN，MN是△OBC的中位线，∴MN∥BC，MN=BC，∴ED∥MN，ED=MN，∴四边形EDNM是平行四边形，由（1）知BD=CE，

又∵OE=ON，OD=OM，OM=BM，ON=CN，∴DM=EN，∴四边形EDNM是矩形，

在△BDC与△CEB中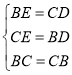， ，∴△BDC≌△CEB，∴∠BCE=∠CBD，∴OB=OC，

∵△ABC的重心到顶点A的距离与底边长相等，∴O到BC的距离=BC，∴BD⊥CE，

∴四边形DEMN是正方形．