【题目】如图,点![]() ,
,![]() ,
,![]() ,
,![]() 是直径为
是直径为![]() 的
的![]() 上的四个点,
上的四个点,![]() 是劣弧
是劣弧![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求证:
,求证:![]() 是正三角形;
是正三角形;
(3)在(2)的条件下,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的面积.
的面积.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)△ACH的面积![]() .
.
【解析】
试题分析:(1)由圆周角定理得出∠DAC=∠CDB,证明△ACD∽△DCE,得出对应边成比例,即可得出结论;
(2)求出DC=![]() ,连接OC、OD,如图所示:证出BC=DC=
,连接OC、OD,如图所示:证出BC=DC=![]() ,由圆周角定理得出∠ACB=90°,由勾股定理得出AB=
,由圆周角定理得出∠ACB=90°,由勾股定理得出AB=![]() =2
=2![]() ,得出OB=OC=OD=DC=BC=
,得出OB=OC=OD=DC=BC=![]() ,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;
,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;
(3)由切线的性质得出OC⊥CH,求出∠H=30°,证出∠H=∠BAC,得出AC=CH=3,求出AH和高,由三角形面积公式即可得出答案.
试题解析:(1)∵C是劣弧![]() 的中点,∴∠DAC=∠CDB,
的中点,∴∠DAC=∠CDB,
∵∠ACD=∠DCE,∴△ACD∽△DCE,∴![]() ,∴DC2=CEAC;
,∴DC2=CEAC;
(2)∵AE=2,EC=1,∴AC=3,∴DC2=CEAC=1×3=3,∴DC=![]() ,
,
连接OC、OD,如图所示:
∵C是劣弧![]() 的中点,∴OC平分∠DOB,BC=DC=
的中点,∴OC平分∠DOB,BC=DC=![]() ,
,
∵AB是⊙O的直径,∴∠ACB=90°,∴AB=![]() =2
=2![]() ,
,
∴OB=OC=OD=DC=BC=![]() ,∴△OCD、△OBC是正三角形,∴∠COD=∠BOC=∠OBC=60°,
,∴△OCD、△OBC是正三角形,∴∠COD=∠BOC=∠OBC=60°,
∴∠AOD=180°﹣2×60°=60°,
∵OA=OD,∴△AOD是正三角形;
(3)∵CH是⊙O的切线,∴OC⊥CH,∵∠COH=60°,∴∠H=30°,
∵∠BAC=90°﹣60°=30°,∴∠H=∠BAC,∴AC=CH=3,
∵AH=3![]() ,AH上的高为BCsin60°=
,AH上的高为BCsin60°=![]() ,∴△ACH的面积=
,∴△ACH的面积=![]() ×3
×3![]() ×
×![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
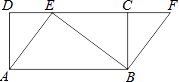
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】“两直线平行,同位角相等”的题设是“两直线平行”,结论是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
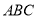 中,
中,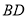 ,
, 分别是两腰上的中线.
分别是两腰上的中线.
(1)求证:
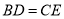 ;
;(2)设
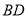 与
与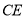 相交于点
相交于点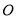 ,点
,点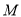 ,
,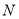 分别为线段
分别为线段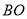 和
和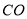 的中点.当
的中点.当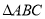 的重心到顶点
的重心到顶点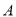 的距离与底边长相等时,判断四边形
的距离与底边长相等时,判断四边形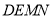 的形状,无需说明理由.
的形状,无需说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=∠A+5°,∠C=∠B+5°,求△ABC的各内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的有( )个
①对顶角相等,邻补角互补
②两条直线被第三条直线所截,同位角的平分线平行
③垂直于同一条直线的两条直线互相平行
④过一点有且只有一条直线与已知直线平行
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“a>b”时,应假设( )
A. a<b B. a≤b C. a≥b D. a≠b
相关试题

