【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF. 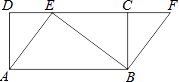
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠BCD=90°.
∴∠BCF=180°﹣∠BCD=180°﹣90°=90°.
∴∠D=∠BCF.在Rt△ADE和Rt△BCF中,
![]()
∴Rt△ADE≌Rt△BCF.
∴∠1=∠F.
∴AE∥BF.
∵AE=BF,
∴四边形ABFE是平行四边形

(2)解:∵∠D=90°,
∴∠DAE+∠1=90°.
∵∠BEF=∠DAE,
∴∠BEF+∠1=90°.
∵∠BEF+∠1+∠AEB=180°,
∴∠AEB=90°.
在Rt△ABE中,AE=3,BE=4,
AB= ![]() .
.
∵四边形ABFE是平行四边形,
∴EF=AB=5
【解析】(1)欲证明四边形ABFE是平行四边形,只要证明AE∥BF,EF∥AB即可.(2)先证明△AEB是直角三角形,再根据勾股定理计算即可.
【考点精析】通过灵活运用平行四边形的判定与性质和矩形的性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长分别是3和7,则其周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+2的图象不经过的象限是( )
A.一
B.二
C.三
D.四 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲开车从距离B市100千米的A市出发去B市,乙从同一路线上的C市出发也去往B市,二人离A市的距离与行驶时间的函数图象如图(y代表距离,x代表时间).

(1)C市离A市的距离是千米;
(2)甲的速度是千米∕小时,乙的速度是千米∕小时;
(3)小时,甲追上乙;
(4)试分别写出甲、乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式.(注明自变量的范围) -
科目: 来源: 题型:
查看答案和解析>>【题目】“两直线平行,同位角相等”的题设是“两直线平行”,结论是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形
 中,
中, ,
, 分别是两腰上的中线.
分别是两腰上的中线.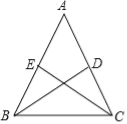
(1)求证:
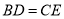 ;
;(2)设
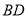 与
与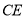 相交于点
相交于点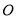 ,点
,点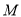 ,
,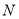 分别为线段
分别为线段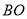 和
和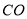 的中点.当
的中点.当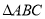 的重心到顶点
的重心到顶点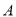 的距离与底边长相等时,判断四边形
的距离与底边长相等时,判断四边形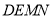 的形状,无需说明理由.
的形状,无需说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 ,
, ,
, ,
, 是直径为
是直径为 的
的 上的四个点,
上的四个点, 是劣弧
是劣弧 的中点,
的中点, 与
与 交于点
交于点 .
. 
(1)求证:
 ;
;(2)若
 ,
, ,求证:
,求证: 是正三角形;
是正三角形;(3)在(2)的条件下,过点
 作
作 的切线,交
的切线,交 的延长线于点
的延长线于点 ,求
,求 的面积.
的面积.
相关试题

