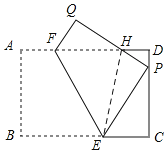
【题目】如图,将矩形纸片ABCD中,AB=6,BC=9,沿EF折叠,使点B落在DC边上点P处,点A落在Q处,AD与PQ相交于点H.

(1)如图1,当点P为边DC的中点时,求EC的长;
(2)如图2,当∠CPE=30°,求EC、AF的长;(3)如图2,在(2)条件下,求四边形EPHF的面积.
参考答案:
【答案】(1)4;(2)6﹣2![]() ;(3)72﹣30
;(3)72﹣30![]()
【解析】
(1)由题意可知PC=3,由翻折的性质可知BE=PE,设EC=x,则PE=9-x,在Rt△PEC中根据勾股定理列方程解答即可;
(2)依据含30°角的直角三角形的性质可知EC与PE关系,设EC=x,则EB=9-x,由翻折的性质可知EP=BE=9-x,列出关于x的方程可求出EC的长,然后利用特殊锐角三角函数值,可求出PC、PD、DH的长,然后设AF=y,由翻折的性质可知AF=QF=y,最后依据FQ=![]() FH列方程解答即可;
FH列方程解答即可;
(3)连接EH,先求出FH和PH、PE的长,最后依据四边形FEPH的面积等于△FHE的面积加△HPE面积求解即可。
解:(1)∵ABCD为矩形,∴CD=AB=6.∵P是DC的中点,∴PC=3.
由翻折的性质可知BE=PE.设EC=x,则PE=9﹣x.
在Rt△PEC中,依据勾股定理可知:PE2=EC2+PC2,即(9﹣x)2=x2+32,解得:x=4,
∴EC=4.
(2)∵∠CPE=30°,∠C=90°,∴EC=![]() PE.
PE.
设EC=x,则EB=9﹣x,由翻折的性质可知EP=BE=9﹣x.
∵EC=![]() PE,∴x=
PE,∴x=![]() ×(9﹣x).解得:x=3.∴EC=3.
×(9﹣x).解得:x=3.∴EC=3.
∴![]() =
=![]() ,则CP=3
,则CP=3![]() .∴DP=6﹣3
.∴DP=6﹣3![]() .∵∠EPH=90°,∠CPE=30°,
.∵∠EPH=90°,∠CPE=30°,
∴∠DPH=60°.∴DH=![]() DP=6
DP=6![]() ﹣9.∴AH=18﹣6
﹣9.∴AH=18﹣6![]() .
.
设AF=y,由翻折的性质可知AF=QF=y,则FH=18﹣6![]() ﹣y.
﹣y.
∵∠QHF=30°,∠Q=90°,∴QF=![]() FH.
FH.
∴y=![]() ×(18﹣6
×(18﹣6![]() ﹣y),解得:y=6﹣2
﹣y),解得:y=6﹣2![]() .
.
∴AF=6﹣2![]()
(3)如图所示:连结EH.
由(2)可知AF=6﹣2![]() ,∴FH=18﹣6
,∴FH=18﹣6![]() ﹣(6﹣2
﹣(6﹣2![]() )=12﹣4
)=12﹣4![]() .
.
∵PH=2DP,EP=2EC,∴PH=12﹣6![]() ,PE=6.
,PE=6.
∴四边形FEPH的面积=△FHE的面积+△HPE的面积=![]() FHAB+
FHAB+![]() HPEP
HPEP
=![]() (12﹣4
(12﹣4![]() )×6+
)×6+![]() ×(12﹣6
×(12﹣6![]() )×6=72﹣30
)×6=72﹣30![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:边长为2的正方形OABC在平面直角坐标系中位于x轴上方,OA与x轴的正半轴的夹角为60°,则B点的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知O为坐标原点,长方形ABCD(点A与坐标原点重合)的顶点D、B分别在x轴、y轴上,且点C的坐标为(-4,8),连接BD,将△ABD沿直线BD翻折至△A
 BD,交CD于点E.
BD,交CD于点E.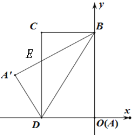
(1)求S△BED的面积;
(2)求点A
 坐标.
坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点B为第一象限内一点,点A为x轴正半轴上一点,分别连接OB,AB,△AOB为等边三角形,点B的横坐标为4.

(1)如图1,求线段OA的长;
(2)如图2,点M在线段OA上(点M不与点O、点A重合),点N在线段BA的延长线上,连接MB,MN,BM=MN,设OM的长为t,BN的长为d,求d与t的关系式(不要求写出t的取值范围);
(3)在(2)的条件下,点D为第四象限内一点,分别连接OD,MD,ND,△MND为等边三角形,线段MA的垂直平分线交OD的延长线于点E,交MA于点H,连接AE,交ND于点F,连接MF,若MF=AM+
 AN,求点E的横坐标.
AN,求点E的横坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.

(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.请画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )

A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
相关试题

