搜索
【题目】已知：边长为2的正方形OABC在平面直角坐标系中位于x轴上方，OA与x轴的正半轴的夹角为60°，则B点的坐标为_____.
参考答案：
【答案】
【解析】
根据“OA与x轴的正半轴的夹角为60°”可知OA与y轴正半轴的夹角为30°，根据正方形的边长为2，和三角函数值可将A点和C点坐标直接求出，将点B坐标设出，根据B到A和C和O的距离，列出方程组即可求出答案。
解：过点A作AM⊥y轴于点M
∵OA与x轴的正半轴的夹角为60°
∴OA与y轴正半轴的夹角为30°，OA=OC=2
∴AM=2xsin30°=1,OM=2xcos30°=
故点A的坐标为（1，）
过点C作CN⊥x轴于点N
∵OC与x轴的夹角为30°
∴CN=2xsin30°=1,ON=2xcos30°=
故点C的坐标为（
）
设点B坐标为（a,b）
过B作BE⊥x轴，交x轴于点E，过C作CD⊥BE，交BE于点D
∵OB=
，BD=b-1，CD=
∴
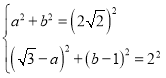
解得
∴点B的坐标为（
）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，方格纸中每个小方格都是边长为1个单位的正方形，若学校位置坐标为A（2，1），图书馆位置坐标为B（﹣1，﹣2），解答以下问题：
（1）在图中标出平面直角坐标系的原点，并建立直角坐标系；
（2）若体育馆位置坐标为C（1，﹣3），请在坐标系中标出体育馆的位置；
（3）顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
小明遇到一个问题：在
中，
，
，
三边的长分别为
、
、
，求的面积．小明是这样解决问题的：如图①所示，先画一个正方形网格（每个小正方形的边长为
），再在网格中画出格点（即三个顶点都在小正方形的顶点处），从而借助网格就能计算出的面积．他把这种解决问题的方法称为构图法．参考小明解决问题的方法，完成下列问题：
（
）图
是一个
的正方形网格（每个小正方形的边长为） ．①利用构图法在答卷的图
中画出三边长分别为、
、
的格点
． ②计算①中
的面积为__________．（直接写出答案）（
）如图
，已知
，以
，
为边向外作正方形
，
，连接
．①判断
与
面积之间的关系，并说明理由．②若
，
，
，直接写出六边形
的面积为__________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一架方梯长25米，如图，斜靠在一面墙上，梯子底端离墙7米．
（1）这个梯子的顶端距地面有多高？
（2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？
（3）当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时，这时梯子的顶端距地面有多高？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知O为坐标原点，长方形ABCD（点A与坐标原点重合）的顶点D、B分别在x轴、y轴上，且点C的坐标为（-4，8），连接BD，将△ABD沿直线BD翻折至△A
BD，交CD于点E．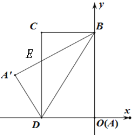
（1）求S△BED的面积；
（2）求点A
坐标. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．
△ACB和△DCE的顶点都在格点上，ED的延长线交AB于点F．
（1）求证：△ACB∽△DCE；（2）求证：EF⊥AB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将矩形纸片ABCD中，AB＝6，BC＝9，沿EF折叠，使点B落在DC边上点P处，点A落在Q处，AD与PQ相交于点H．
（1）如图1，当点P为边DC的中点时，求EC的长；
（2）如图2，当∠CPE＝30°，求EC、AF的长；（3）如图2，在（2）条件下，求四边形EPHF的面积．
相关试题
