搜索
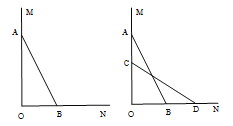
【题目】（本题6分）如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AO上，这时梯足B到墙底端O的距离为0.7米, 如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？
参考答案：
【答案】0.8米
【解析】
试题首先根据Rt△AOB的勾股定理求出AO的长度，然后计算出OC的长度，根据Rt△COD的勾股定理求出OD的长度，最后根据BD=OD－0B进行求解.
试题解析：由题意，在Rt△AOB中，AB=2.5米，BO=0.7米
由勾股定理得AO=
=2.4米
∴CO=AO－AC=2.4－0.4=2米
在Rt△COD中，CD=2.5米，CO=2米 由勾股定理得OD=
=1.5米
∴BD=OD-OB=1.5－0.7=0.8米
答：梯足将向外移0.8米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】“科学”号是我国目前最先进的海洋科学综合考察船，它在南海利用探测仪在海面下方探测到点C处有古代沉船．如图，海面上两探测点A，B相距1400米，探测线与海面的夹角分别是30°和60°．试确定古代沉船所在点C的深度．（结果精确到1米，参考数据：
≈1.414， 
≈1.732）
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题：
（1）（﹣1）2018﹣2（π﹣1）0+（﹣
）﹣2（2）（2a﹣4）（
a+5）﹣2（a﹣10）（3）（2x+3y）（﹣2x+3y）﹣（x﹣3y）2
（4）（4x3y﹣6x2y2+12xy3）÷2xy
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，四边形ABCD是菱形，AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M，连接BM，且AH=3．
（1）求证:DM=BM；
（2）求MH的长；
（3）如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式；
（4）在（3）的条件下，当点P在边AB上运动时是否存在这样的 t值，使∠MPB与∠BCD互为余角，若存在,则求出t值，若不存，在请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在⊙O中，OE垂直于弦AB，垂足为点D，交⊙O于点C，∠EAC=∠CAB．
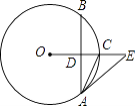
（1）求证：直线AE是⊙O的切线；
（2）若AB=8，sin∠E=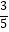
，求⊙O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】码头工人每天往一艘轮船50吨货物，装载完毕恰好用了8天时间．
（1）轮船到达目的地后开始卸货，平均卸货速度v（单位：吨/天）与卸货时间t（单位：天）之间有怎样的函数关系？
（2）由于遇到紧急情况，要求船上的货物不超过5天卸货完毕，那么平均每天至少要卸多少吨货物？
（3）若原有码头工人10名，在（2）的条件下，至少需要增加多少名工人才能完成任务？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在矩形ABCD中，BC=2CD=2a，点E在边CD上，在矩形ABCD的左侧作矩形ECGF，使CG=2GF=2b，连接BD，CF，连结AF交BD于点H．
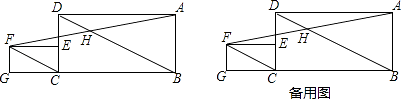
（1）求证：BD∥CF；
（2）求证：H是AF的中点；
（3）连结CH，若HC⊥BD，求a：b的值．
相关试题
