【题目】码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?
参考答案:
【答案】
(1)解:∵50×8=400,
根据题意得:v= ![]() ,
,
∴速度v(单位:吨/天)与卸贺时间t(单位:天)之间的函数关系为:v= ![]() ;
;
(2)解:∵t=5,
∴v= ![]() ,
,
解得:v=80,
答:平均每天至少要卸80吨货物;
(3)解:∵每人一天可卸货:50÷10=5(吨),
∴80÷5=16(人)
16﹣10=6(人).
答:码头至少需要再增加6名工人才能按时完成任务.
【解析】(1)根据题意可知速度v与卸贺时间t之间是反比例函数关系,则可求得答案。
(2)将t=5,代入函数解析式即可求得v的值,即求得平均每天至少要卸的货物。
(3)由10名工人,每天一共可卸货50吨,即可得出平均每人卸货的吨数,从而求得答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AO上,这时梯足B到墙底端O的距离为0.7米, 如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
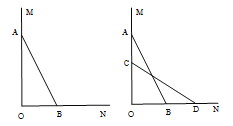
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,OE垂直于弦AB,垂足为点D,交⊙O于点C,∠EAC=∠CAB.
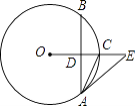
(1)求证:直线AE是⊙O的切线;
(2)若AB=8,sin∠E=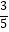 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.
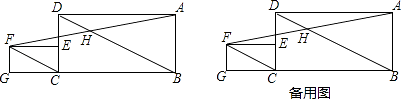
(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2( ),
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠3( )
又∵∠B=∠C(已知)
∴∠3=∠B( )
∴AB∥CD( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1) 是描述小凡的运动过程(填
 或
或 );
);(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)

相关试题

