Question

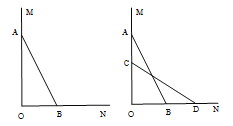
【题目】“科学”号是我国目前最先进的海洋科学综合考察船，它在南海利用探测仪在海面下方探测到点C处有古代沉船．如图，海面上两探测点A，B相距1400米，探测线与海面的夹角分别是30°和60°．试确定古代沉船所在点C的深度．（结果精确到1米，参考数据： ≈1.414， ≈1.732）

Answer 1

【答案】解：如图所示：过点C作CD⊥AB于点D，

由题意可得：∠DAC=30°，∠DBC=60°，AB=1400km，

则∠BCA=30°，

故AB=BC=1400km，

sin60°= = ，

解得：DC=700 ≈1212（km）．

答：古代沉船所在点C的深度约为1212km．

【解析】根据题意添加辅助线，过点C作CD⊥AB于点D，先证明AB=BC，然后在Rt△DBC中，利用∠DBC的正弦求出DC的长。
【考点精析】通过灵活运用锐角三角函数的定义和特殊角的三角函数值，掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”即可以解答此题．