【题目】蜗牛从某点开始沿一条东西方向的直线爬行,规定以出发点为原点,向东爬行的路程记为正数,向西爬行的路程记为负数,则蜗牛爬过的各段路程依次为+5,-3,+10,-8,-6,+12,-10.(单位:厘米)
(1)请判断蜗牛最后是否回到出发点?
(2)蜗牛离开出发点0最远时是多少厘米?
(3)在爬行过程中,若蜗牛每爬1厘米就奖励一粒芝麻,则蜗牛一共得到多少粒芝麻?
参考答案:
【答案】(1)蜗牛最后回到了出发点(2)最远是12厘米(3)![]() 粒
粒
【解析】
(1)计算出它爬行所有数的和,再与0比较即可判断是否回到出发点;
(2)分别计算出每次爬行后距离O点的距离,再比较即可;
(3)计算所有数的绝对值的和得到小虫爬行的路程,再把路程乘以1得到蜗牛共得的芝麻粒数.
解:(1)+5+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=5-3+10-8-6+12-10=0,
∴蜗牛最后是否回到出发点;
(2)如下表:
移动 | 5 | -3 | +10 | -8 | -6 | +12 | -10 |
停留位置 | 5 | 2 | 12 | 4 | -2 | 10 | 0 |
由表知,最远是12厘米;
(3)![]() ,
,
∴蜗牛一共得到54粒芝麻.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了某校七年级学生对
 《最强大脑》、
《最强大脑》、 《朗读者》、
《朗读者》、 《中国诗词大会》、
《中国诗词大会》、 《极限挑战》四个电视节目的喜爱情况,随机抽取了
《极限挑战》四个电视节目的喜爱情况,随机抽取了 位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)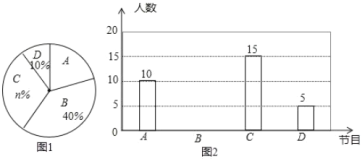
根据统计图提供的信息,回答下列问题:
(1)
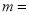 ______,
______,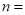 ______.
______.(2)在图1中,喜爱《朗读者》节目所对应的扇形的圆心角度数是______度;
(3)请根据以上信息直接在答题卡中补全图2的条形统计图;
(4)已知该校七年级共有420位学生,那么他们最喜欢《中国诗词大会》这个节目的学生约有多少人?
-
科目: 来源: 题型:
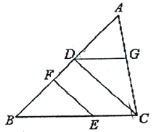
查看答案和解析>>【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,
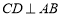 ,
,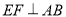 ,垂足分别为D、F,
,垂足分别为D、F,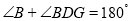 ,请试说明
,请试说明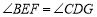 .
.
证明:∵
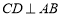 ,
,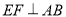 (已知)
(已知)∴
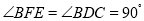 (____________________________)
(____________________________)∴
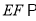 ________(____________________________)
________(____________________________)∴
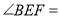 ________(____________________________)
________(____________________________)又∵
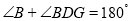 (已知)
(已知)∴
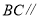 ________(____________________________)
________(____________________________)∴
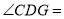 ________(____________________________)
________(____________________________)∴
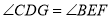 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周)
小明抽样人数
小华抽样人数
0~1
6
22
1~2
10
10
2~3
16
6
3~4
8
2
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是用棋子摆成的“
 ”字形图案.
”字形图案.
(1)填写下表:
图案序号
①
②
③
④
…
⑩
每个图案中棋子的个数
5
8
…
(2)第
 个“
个“ ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含 的代数式表示)
的代数式表示)(3)第20个“
 ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?(4)计算前20个“
 ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______ -
科目: 来源: 题型:
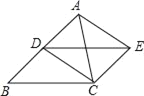
查看答案和解析>>【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.
相关试题

