【题目】为了某校七年级学生对![]() 《最强大脑》、
《最强大脑》、![]() 《朗读者》、
《朗读者》、![]() 《中国诗词大会》、
《中国诗词大会》、![]() 《极限挑战》四个电视节目的喜爱情况,随机抽取了
《极限挑战》四个电视节目的喜爱情况,随机抽取了![]() 位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
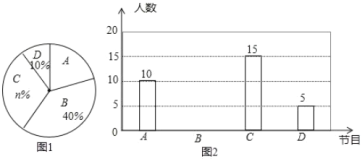
根据统计图提供的信息,回答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在图1中,喜爱《朗读者》节目所对应的扇形的圆心角度数是______度;
(3)请根据以上信息直接在答题卡中补全图2的条形统计图;
(4)已知该校七年级共有420位学生,那么他们最喜欢《中国诗词大会》这个节目的学生约有多少人?
参考答案:
【答案】(1)50,30(2)144(3)作图见解析(4)126
【解析】
(1)根据《极限挑战》的人数除以占的百分比求出调查的总人数,再有《中国诗词大会》的人数即可求出n的值;
(2)求出喜爱《朗读者》节目人数的百分比,乘以360即可得到结果;
(3)补全条形统计图,如图所示;
(4)由420乘以喜欢《中国诗词大会》的百分比即可得到结果.
解:(1)![]() 人,
人,![]() ,
,
故答案为:50,30,
(2)![]() ,
,
故答案为:144.
(3)![]() ,补全统计图如图所示:
,补全统计图如图所示:
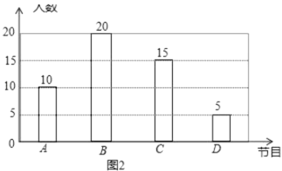
(4)![]() 人,
人,
故答案为:126.
-
科目: 来源: 题型:
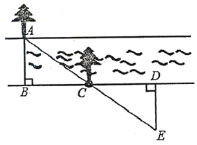
查看答案和解析>>【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一侧岸边B点,选对岸正对的一棵树A;
②沿河岸直走20米有一树C,继续前行20米到达D处;
③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求河流的宽度是多少?并说明理由.
-
科目: 来源: 题型:
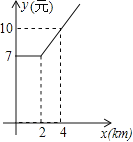
查看答案和解析>>【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.

-
科目: 来源: 题型:
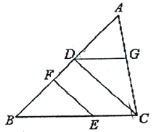
查看答案和解析>>【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,
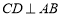 ,
,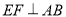 ,垂足分别为D、F,
,垂足分别为D、F,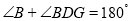 ,请试说明
,请试说明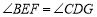 .
.
证明:∵
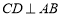 ,
,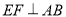 (已知)
(已知)∴
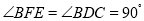 (____________________________)
(____________________________)∴
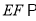 ________(____________________________)
________(____________________________)∴
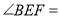 ________(____________________________)
________(____________________________)又∵
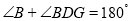 (已知)
(已知)∴
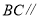 ________(____________________________)
________(____________________________)∴
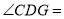 ________(____________________________)
________(____________________________)∴
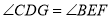 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点开始沿一条东西方向的直线爬行,规定以出发点为原点,向东爬行的路程记为正数,向西爬行的路程记为负数,则蜗牛爬过的各段路程依次为+5,-3,+10,-8,-6,+12,-10.(单位:厘米)
(1)请判断蜗牛最后是否回到出发点?
(2)蜗牛离开出发点0最远时是多少厘米?
(3)在爬行过程中,若蜗牛每爬1厘米就奖励一粒芝麻,则蜗牛一共得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周)
小明抽样人数
小华抽样人数
0~1
6
22
1~2
10
10
2~3
16
6
3~4
8
2
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
相关试题

