【题目】两个大小不同的等腰直角三角形三角板按图1所示的位置放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.
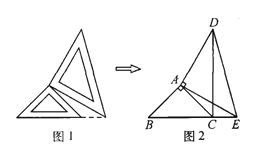
(1)请找出图2中与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
参考答案:
【答案】(1)△ACD≌△ABE.证明见解析;(2)证明见解析.
【解析】
试题分析:根据等腰直角三角形的性质利用SAS判定△ABE≌△ACD;因为全等三角形的对应角相等,所以∠ACD=∠ABE=45°,已知∠ACB=45°,所以可得到∠BCD=∠ACB+∠ACD=90°,即DC⊥BE.
试题解析:(1)解:图2中△ACD≌△ABE.
证明:∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°.
∴∠BAC+∠CAE=∠EAD+∠CAE.
即∠BAE=∠CAD.
∵在△ABE与△ACD中,
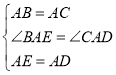
∴△ABE≌△ACD(SAS);
(2)证明:由(1)△ABE≌△ACD,
则∠ACD=∠ABE=45°.
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°.
∴DC⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】坐标平面上,某个一次函数的图形通过(5,0)、(10,﹣10)两点,判断此函数的图形会通过下列哪一点?( )
A.( ,9
,9  )
)
B.( ,9
,9  )
)
C.( ,9
,9  )
)
D.(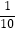 ,9
,9 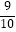 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】表为甲班55人某次数学小考成绩的统计结果,关于甲班男、女生此次小考成绩的统计量,下列叙述何者正确?( )
成绩(分)
50
70
90
男生(人)
10
10
10
女生(人)
5
15
5
合计(人)
15
25
15
A.男生成绩的四分位距大于女生成绩的四分位距
B.男生成绩的四分位距小于女生成绩的四分位距
C.男生成绩的平均数大于女生成绩的平均数
D.男生成绩的平均数小于女生成绩的平均数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=60°,∠B=58°.甲、乙两人想在△ABC外部取一点D,使得△ABC与△DCB全等,其作法如下:
(甲)①作∠A的角平分线L.
②以B为圆心,BC长为半径画弧,交L于D点,则D即为所求.
(乙)①过B作平行AC的直线L.
②过C作平行AB的直线M,交L于D点,则D即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )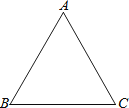
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
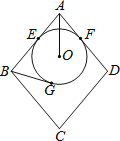
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=45°,
∠F=30°,∠CGF=70°,求∠A的度数.
(2)利用三角板也能画出一个角的平分线,画法如下:①利用三角板在∠AOB的两边上分
别取OM=ON:②分别过点M、N画OM、ON的垂线,交点为
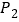 ;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.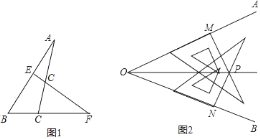
相关试题

