搜索
【题目】如图，菱形ABCD的边长为10，圆O分别与AB、AD相切于E、F两点，且与BG相切于G点．若AO=5，且圆O的半径为3，则BG的长度为何？（ ）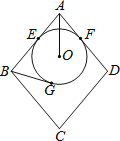 
A.4
B.5
C.6
D.7
参考答案：
【答案】C
【解析】解：连接OE，
∵⊙O与AB相切于E，
∴∠AEO=90°，
∵AO=5，OE=3，
∴AE= 
=4，
∵AB=10，
∴BE=6，
∵BG与⊙O相切于G，
∴BG=BE=6，
故选C．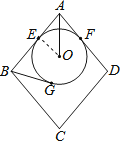
【考点精析】本题主要考查了菱形的性质和切线的性质定理的相关知识点，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠A=60°，∠B=58°．甲、乙两人想在△ABC外部取一点D，使得△ABC与△DCB全等，其作法如下：
（甲）①作∠A的角平分线L．
②以B为圆心，BC长为半径画弧，交L于D点，则D即为所求．
（乙）①过B作平行AC的直线L．
②过C作平行AB的直线M，交L于D点，则D即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）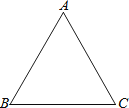
A.两人皆正确
B.两人皆错误
C.甲正确，乙错误
D.甲错误，乙正确 -
科目： 来源： 题型：
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板按图1所示的位置放置，图2是由它抽象出的几何图形，AB=AC，AE=AD，∠BAC=∠EAD=90°，B，C，E在同一条直线上，连接DC．
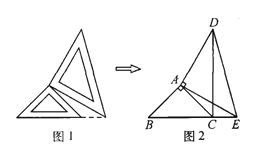
（1）请找出图2中与△ABE全等的三角形，并给予证明；
（2）证明：DC⊥BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，甲出发1h后，乙出发．设甲与A地相距y甲（km），乙与A地相距y乙（km），甲离开A地时间为x（h），y甲、y乙与x之间的函数图象如图所示．
（1）甲的速度是 km/h．
（2）请分别求出y甲、y乙与x之间的函数关系式．
（3）当乙与A地相距240km时，甲与B地相距多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1在△ABC中，EF与AC交于点G，与BC的延长线交于点F，∠B=45°，
∠F＝30°，∠CGF＝70°，求∠A的度数.
（2）利用三角板也能画出一个角的平分线，画法如下：①利用三角板在∠AOB的两边上分
别取OM＝ON：②分别过点M、N画OM、ON的垂线，交点为
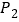；③画射线OP，所以射线OP为∠AOB的角平分线，请你评判这种作法的正确性并说明理由.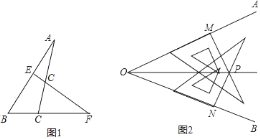
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数，且皆有31项．若a2+b30=29，a30+b2=﹣9，则此两等差级数的和相加的结果为多少？（ ）
A.300
B.310
C.600
D.620 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中的位置如图所示，直线l过点M（3，0）且平行于y轴．
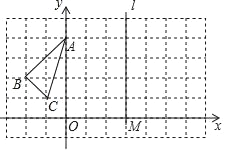
（1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标．
（2）如果点P的坐标是（﹣a，0），其中a＞0，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求P1P2的长．（用含a的代数式表示）
（3）通过计算加以判断，PP2的长会不会随点P位置的变化而变化．
相关试题
