【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
参考答案:
【答案】(1)![]() ;(2)仅从工资收入的角度考虑,小明应到乙公司应聘.
;(2)仅从工资收入的角度考虑,小明应到乙公司应聘.
【解析】
(1)根据概率公式计算可得;
(2)分别根据平均数的定义及其意义解答可得.
(1)因为今年四月份甲公司揽件员人均揽件数超过40的有4天,
所以甲公司揽件员人均揽件数超过40(不含40)的概率为![]() ;
;
(2)①甲公司各揽件员的日平均件数为![]() =39件;
=39件;
②甲公司揽件员的日平均工资为70+39×2=148元,
乙公司揽件员的日平均工资为![]()
=[40+![]() ]×4+
]×4+![]() ×6
×6
=159.4元,
因为159.4>148,
所以仅从工资收入的角度考虑,小明应到乙公司应聘.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等边三角形
 沿着
沿着 折叠,使点
折叠,使点 恰好落在
恰好落在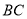 边上的点
边上的点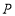 处,且
处,且 。若
。若 ,
, ,则
,则 ______
______ .(在直角三角形中,
.(在直角三角形中, 角所对的直角边等于斜边的一半。)
角所对的直角边等于斜边的一半。)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边
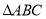 中,点
中,点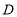 、
、 分别在
分别在 、
、 上,
上, ,连
,连 、
、 .
.
(1)求证:
 ;
;(2)如图2,延长
 至点
至点 ,使得
,使得 ,连
,连 ,试判断
,试判断 的形状,并说明理由;
的形状,并说明理由;(3)在(2)的条件下,连
 ,
, .若
.若 ,则
,则 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+
 ∠C;
∠C;②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )

A.①②B.③④C.①②④D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
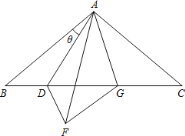
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

相关试题

