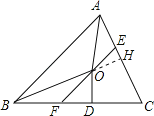
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;
∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )

A.①②B.③④C.①②④D.①③④
参考答案:
【答案】C
【解析】
根据角平分线的定义和三角形内角和定理判断①;根据角平分线的定义和平行线的性质判断②;根据三角形三边关系判断③;根据角平分线的性质判断④.
∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=![]() ∠CBA,∠OAB=
∠CBA,∠OAB=![]() ∠CAB,
∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB
=180°﹣![]() ∠CBA﹣
∠CBA﹣![]() ∠CAB
∠CAB
=180°﹣![]() (180°﹣∠C)
(180°﹣∠C)
=90°+![]() ∠C,①正确;
∠C,①正确;
∵EF∥AB,
∴∠FOB=∠ABO,又∠ABO=∠FBO,
∴∠FOB=∠FBO,
∴FO=FB,
同理EO=EA,
∴AE+BF=EF,②正确;
当∠C=90°时,AE+BF=EF<CF+CE,
∴E,F不是AC,BC的中点,③错误;
作OH⊥AC于H,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OD=OH,
∴S△CEF=![]() ×CF×OD
×CF×OD![]() ×CE×OH=ab,④正确.
×CE×OH=ab,④正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等边三角形
 沿着
沿着 折叠,使点
折叠,使点 恰好落在
恰好落在 边上的点
边上的点 处,且
处,且 。若
。若 ,
, ,则
,则 ______
______ .(在直角三角形中,
.(在直角三角形中, 角所对的直角边等于斜边的一半。)
角所对的直角边等于斜边的一半。)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边
 中,点
中,点 、
、 分别在
分别在 、
、 上,
上, ,连
,连 、
、 .
.
(1)求证:
 ;
;(2)如图2,延长
 至点
至点 ,使得
,使得 ,连
,连 ,试判断
,试判断 的形状,并说明理由;
的形状,并说明理由;(3)在(2)的条件下,连
 ,
, .若
.若 ,则
,则 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
-
科目: 来源: 题型:
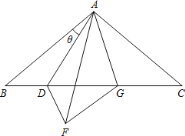
查看答案和解析>>【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
相关试题

