【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数 ![]() 与方差s2:
与方差s2:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2(cm2) | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁
参考答案:
【答案】A
【解析】解:∵甲的方差是3.5,乙的方差是3.5,丙的方差是15.5,丁的方差是16.5,
∴S甲2=S乙2<S丙2<S丁2,
∴发挥稳定的运动员应从甲和乙中选拔,
∵甲的平均数是561,乙的平均数是560,
∴成绩好的应是甲,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择甲;
所以答案是:A.
【考点精析】关于本题考查的算术平均数,需要了解总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 , 它(填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图1在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.
(1)若BF=5,DC=3,求AB的长;
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,链条垂线交于点G,连接BG,得如图2.
①求证:∠BGF=45°;
②求证:AB=AG+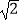 AF.
AF.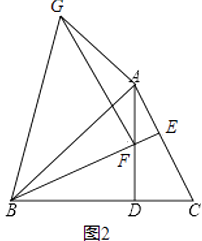
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),平面直角坐标系中,一次函数y=﹣x+1的图象与y轴交于点A,点B是第二象限一次函数y=﹣x+1的图象上一点,且S△OAB=3,点C的坐标为(﹣2,﹣3).
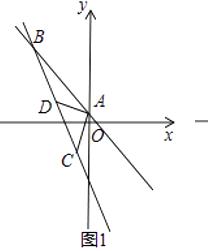
(1)求A,B的坐标;
(2)如图(1)若点D是线段BC上一点,且三角形ABD的面积是三角形ABC的一半,求△ABC的面积和点D的坐标;
(3)在(2)的条件下,如图(2),将线段AC沿直线AB平移,点A的对应点为A1 , 点C的对应点为C1 , 连接A1D,C1D,当△A1C1D直角三角形时,求A1的坐标.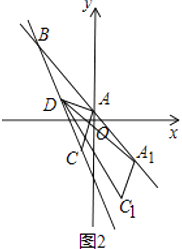
-
科目: 来源: 题型:
查看答案和解析>>【题目】天义地区某天的最高气温是8℃,最低气温是﹣2℃,则该地这一天的温差是( )
A.10℃
B.﹣6℃
C.6℃
D.﹣10℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是三角形的三边,那么代数式(a﹣b)2﹣c2的值( )
A. 大于零 B. 小于零 C. 等于零 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形,下列说法:
①如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是平行四边形.
②如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是菱形
③在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,则中点四边形EFGH是正方形
其中,正确的有( )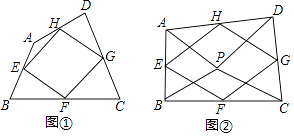
A.0个
B.1个
C.2个
D.3个
相关试题

