【题目】如图1,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE:CE=3:2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)线段AE= ;
(2)设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
(3)当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径;
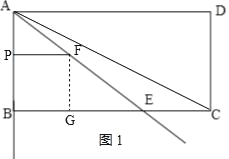
(4)如图2,将△AEC沿直线AE翻折,得到△AEC',连结AC',如果∠ABF=∠CBC′,求t值.(直接写出答案,不要求解答过程).

参考答案:
【答案】(1)5;(2)y=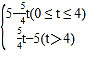 ;(3)12;(4)
;(3)12;(4)![]() .
.
【解析】(1)由矩形性质知BC=AD=5,根据BE:CE=3:2知BE=3,利用勾股定理可得AE=5;
(2)由PF∥BE知![]() ,据此求得AF=
,据此求得AF=![]() t,再分0≤t≤4和t>4两种情况分别求出EF即可得;
t,再分0≤t≤4和t>4两种情况分别求出EF即可得;
(3)由以点F为圆心的⊙F恰好与直线AB、BC相切时PF=PG,再分t=0或t=4、0<t<4、t>4这三种情况分别求解可得;
(4)连接CC′,交直线AE于点Q,先证△CQE∽△ABE得![]() ,据此求得CQ=
,据此求得CQ=![]() 、CC′=2CQ=
、CC′=2CQ=![]() ,再证△ABF∽△CBC′得
,再证△ABF∽△CBC′得![]() ,据此求得AF=
,据此求得AF=![]() ,根据
,根据![]() 可得答案.
可得答案.
(1)∵四边形ABCD为矩形,
∴BC=AD=5,
∵BE:CE=3:2,
则BE=3、CE=2,
∴AE=![]() =5,
=5,
故答案为:5;
(2)如图1,当点P在线段AB上运动时,即0≤t≤4,
∵PF∥BE,
∴![]() ,即
,即![]() ,
,
∴AF=![]() ,
,
则EF=AE﹣AF=5﹣![]() ,即y=5﹣
,即y=5﹣![]() (0≤t≤4);
(0≤t≤4);
如图2,当点P在射线AB上运动时,即t>4,
此时EF=AF﹣AE=![]() ﹣5,即y=
﹣5,即y=![]() ﹣5 (t>4);
﹣5 (t>4);
综上,y=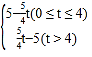 ;
;
(3)以点F为圆心的⊙F恰好与直线AB、BC相切时,PF=PG,
分以下三种情况:①当t=0或t=4时,显然符合条件的⊙F不存在;
②当0<t<4时,如图1,作FG⊥BC于点G,
则FG=BP=4﹣t,
∵PF∥BC,
∴△APF∽△ABE,
∴![]() ,即
,即![]() ,
,
∴PF=![]() t,
t,
由4﹣t=![]() t可得t=
t可得t=![]() ,
,
则此时⊙F的半径PF=![]() ;
;
③当t>4时,如图2,同理可得FG=t﹣4、PF=![]() t,
t,
由t﹣4=![]() t可得t=16,
t可得t=16,
则此时⊙F的半径PF=12;
(4)如图3,连接CC′,交直线AE于点Q,
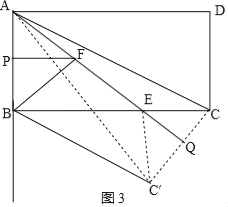
∵△CAQ≌△C′AQ,
∴AC=AC′、∠CAQ=∠C′AQ,
则∠CQE=∠ABE=90°,
∵∠CEQ=∠AEB,
∴△CQE∽△ABE,
∴![]() ,即
,即![]() ,
,
∴CQ=![]() ,
,
则CC′=2CQ=![]() ,
,
∵∠ABF=∠CBC′、∠BAE=∠ECC′,
∴△ABF∽△CBC′,
∴![]() ,即
,即![]() ,
,
解得: AF=![]() ,
,
由(2)知AF=![]() t,
t,
∴![]() ,
,
解得:t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字-2、l、2,它们除了数字不同外,其它都完全相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字l的小球的概率为 .
(2)小红先从布袋中随机摸出一个小球,记下数字作为
 的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为
的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为 的值,请用树状图或表格列出
的值,请用树状图或表格列出 、
、 的所有可能的值,并求出直线
的所有可能的值,并求出直线 不经过第四象限的概率.
不经过第四象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,D为△ABC的边AB的延长线上一点,过D作DF⊥AC,垂足为F,交BC于E,且BD=BE,求证:△ABC是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
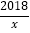 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
相关试题

