【题目】菱形ABCD中,AB=5,AE是BC边上的高,AE=4,则对角线BD的长为_____.
参考答案:
【答案】2![]() 或4
或4![]()
【解析】
分∠B为钝角和锐角两种情况,在Rt△ABE中求得BE,则可求得EC,在Rt△AEC中利用勾股定理可求得AC,再利用等积法可求得BD的长.
解:当∠B为钝角时,如图1,
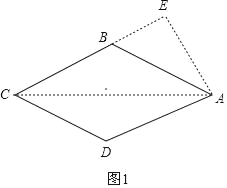
∵AB=5,AE=4,且AE⊥BC,
∴BE=3,
∴CE=BC+BE=5+3=8,
在Rt△ACE中,由勾股定理可得AC=![]() =4
=4![]() ,
,
∵S菱形ABCD=BCAE=![]() BDAC,
BDAC,
∴5×4=![]() ×4
×4![]() BD,解得BD=2
BD,解得BD=2![]() ;
;
当∠B为锐角时,如图2,
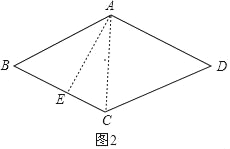
同理可求得BE=3,则CE=5﹣3=2,
在Rt△ACE中,可求得AC=![]() =2
=2![]() ,
,
同理可求得BD=4![]() ,
,
综上可知BD的长为2![]() 或4
或4![]() ,
,
故答案为:2![]() 或4
或4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,如图,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC,
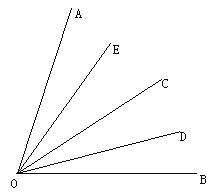
(1)求∠DOE的度数;
(2)当OC在∠AOB内绕O点旋转时,OD、OE仍是∠BOC和∠AOC的平分线,问此时∠DOE的大小是否和(1)中的答案相同?通过此过程,你能总结出怎样的结论?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
-
科目: 来源: 题型:
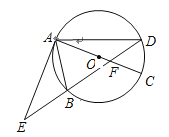
查看答案和解析>>【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县某初中为了创建书香校园,购进了一批图书.其中的20本某种科普书和30本某种文学书共花了1080元,经了解,购买的科普书的单价比文学书的单价多4元.
(1)购买的科普书和文学书的单价各多少元?
(2)另一所学校打算用800元购买这两种图书,问购进25本文学书后至多还能购进多少本科普书?
相关试题

