【题目】已知∠AOB=80°,如图,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC,
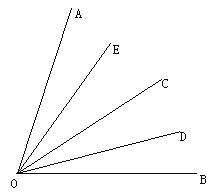
(1)求∠DOE的度数;
(2)当OC在∠AOB内绕O点旋转时,OD、OE仍是∠BOC和∠AOC的平分线,问此时∠DOE的大小是否和(1)中的答案相同?通过此过程,你能总结出怎样的结论?
参考答案:
【答案】(1)∠DOE=40°;(2)∠DOE大小不变,结论:OC不论怎样变化,只要∠AOB不变,总有∠DOE=∠AOB.
【解析】
(1)根据角平分线的定义求得∠AOC=∠BOD=![]() ∠AOB=
∠AOB=![]() ×80°=40,再由角平分线的定义求得,∠DOC=
×80°=40,再由角平分线的定义求得,∠DOC=![]() ∠BOC=
∠BOC=![]() ×40°=20°,∠EOC=
×40°=20°,∠EOC=![]() ∠AOC=
∠AOC=![]() ×40°=20°,即可求解;
×40°=20°,即可求解;
(2)根据角平分线的定义求得,∠DOE=∠DOC+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB,从而解决问题.
∠AOB,从而解决问题.
解:(1)∵OC是∠AOB的平分线 ,
∴∠AOC=∠BOD=![]() ∠AOB=
∠AOB=![]() ×80°=40°,
×80°=40°,
∵OD、OE分别平分∠BOC、∠AOC ,
∴∠DOC=![]() ∠BOC=
∠BOC=![]() ×40°=20°,
×40°=20°,
∠EOC=![]() ∠AOC=
∠AOC=![]() ×40°=20°,
×40°=20°,
∴∠DOE=∠DOC=∠EOC=20°+20°=40°.
(2)当OC旋转时,
∵OD、OE仍为∠BOC、∠AOC的平分线,
∴∠DOC=![]() ∠BOC,∠EOC=
∠BOC,∠EOC=![]() ∠AOC,
∠AOC,
∴∠DOE=∠DOC+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=
∠AOB=![]() ×80°=40°,
×80°=40°,
∴∠DOE大小不变,
∴OC不论怎样变化,只要∠AOB不变,总有∠DOE=∠AOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=
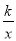 图象上.
图象上.(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
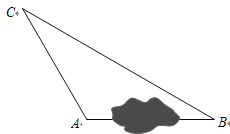
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8
 B. 8 C. 4
B. 8 C. 4 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并将它的解集在数轴上表示出来.
,并将它的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,AB=5,AE是BC边上的高,AE=4,则对角线BD的长为_____.
相关试题

