【题目】如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以lcms的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.
(1)若点F的运动速度与点E的运动速度相等,当t=2时:
①判断△BEF与△ADE是否全等?并说明理由;
②求∠EDF的度数.
(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.

参考答案:
【答案】(1)①△BEF≌△ADE;②由①得DE=EF,∠BEF=∠ADE;(2)存在,①如图2,当△DAE≌△EBF时,x=1,t=2;②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,x=![]() ,t=
,t=![]() .
.
【解析】
![]() 根据SAS证明:
根据SAS证明:![]() ≌
≌![]() ;
;![]() 由
由![]() :
:![]() ≌
≌![]() 得
得![]() ,
,![]() ,证明
,证明![]() 是等腰直角三角形可得结论;
是等腰直角三角形可得结论;![]() 分两种情况:
分两种情况:![]() 如图2,当
如图2,当![]() ≌
≌![]() 时,
时,![]() 如图3,当
如图3,当![]() ≌
≌![]() 时,分别根据
时,分别根据![]() ,
,![]() ,列方程组可得结论.
,列方程组可得结论.
解:(1)①△BEF≌△ADE,理由如:
当t=2时,AE=BF=2,
∴BE=AB-AD=7-2=5,
∵AD=5,
∴BE=AD,
∵∠A=∠B=90°,
∴△BEF≌△ADE;
②由①得DE=EF,∠BEF=∠ADE,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠BEF+∠AED=90°,
∴∠DEF=180°-(∠BEF+∠AED)=90°,
∵DE=EF
∴∠EDF=∠EFD,
∵∠EDF+∠EFD=90°,
∴∠EDF=45°;
(2)存在,
①如图2,当△DAE≌△EBF时,
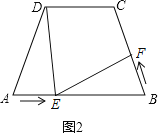
∴AD=BE,AE=BF,
则![]()
∴x=1,t=2;
②如图3,当△ADE≌△BFE时,AE=BE,AD=BF,
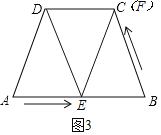
则![]() ,
,
∴x=![]() ,t=
,t=![]() .
.
-
科目: 来源: 题型:
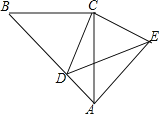
查看答案和解析>>【题目】如图,△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,且点D在线段AB上,连接AE.
(1)求证:①△BCD≌△ACE;②∠DAE=90°;
(2)若AB=8,当点D在线段AB上什么位置时,四边形ADCE的周长最小?请说明并求出周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
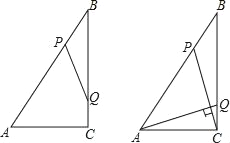
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,

(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG2=BFBO.试证明BG=PG;
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=
 .求弦CD的长.
.求弦CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
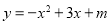 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

相关试题

