【题目】如图，二次函数的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点．

（1）求m的值及C点坐标；

（2）在直线BC上方的抛物线上是否存在一点M，使得它与B，C两点构成的三角形面积最大，若存在，求出此时M点坐标；若不存在，请简要说明理由；

（3）P为抛物线上一点，它关于直线BC的对称点为Q．

①当四边形PBQC为菱形时，求点P的坐标；

②点P的横坐标为t（0＜t＜4），当t为何值时，四边形PBQC的面积最大，请说明理由．

参考答案：

【答案】（1）m=4，C（0，4）；（2）存在，M（2，6）；（3）①P（，）或P（，）；②当t=2时，S四边形PBQC最大=16．

【解析】

试题分析：（1）用待定系数法求出抛物线解析式；

（2）先判断出面积最大时，平移直线BC的直线和抛物线只有一个交点，从而求出点M坐标；

（3）①先判断出四边形PBQC时菱形时，点P是线段BC的垂直平分线，利用该特殊性建立方程求解；

②先求出四边形PBCQ的面积与t的函数关系式，从而确定出它的最大值．

试题解析：（1）将B（4，0）代入，解得，m=4，∴二次函数解析式为，令x=0，得y=4，∴C（0，4）；

（2）存在，理由：∵B（4，0），C（0，4），∴直线BC解析式为y=﹣x+4，当直线BC向上平移b单位后和抛物线只有一个公共点时，△MBC面积最大，∴，∴，∴△=16﹣4b=0，∴b=4，∴，∴M（2，6）；

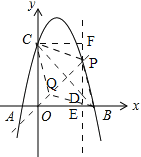
（3）①如图，∵点P在抛物线上，∴设P（m，），当四边形PBQC是菱形时，点P在线段BC的垂直平分线上，∵B（4，0），C（0，4），∴线段BC的垂直平分线的解析式为y=x，∴m=，∴m=，∴P（，）或P（，）；

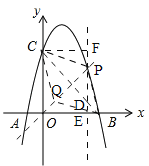
②如图，设点P（t，），过点P作y轴的平行线l，过点C作l的垂线，∵点D在直线BC上，∴D（t，﹣t+4），∵PD=﹣（﹣t+4）=，BE+CF=4，∴S四边形PBQC=2S△PDC=2（S△PCD+S△BD）=2（PD×CF+PD×BE）=4PD==，∵0＜t＜4，∴当t=2时，S四边形PBQC最大=16．

关闭