【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.

(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)直线BC的解析式为y=﹣![]() x+
x+![]() ;(2)P(
;(2)P(![]() ,
,![]() ),PE+
),PE+![]() BE=
BE=![]() ;(3)存在,Q(﹣1,
;(3)存在,Q(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ),理由见解析
),理由见解析
【解析】
(1)根据二次函数的解析式先求出点C、点B的坐标,然后利用待定系数法即可求出直线BC的解析式;
(2)如图2中,过点P作PM⊥x轴于点M,交直线BC于点F,过点E作EN⊥x轴于点N,设P(a,﹣![]() a2+
a2+![]() a+
a+![]() ),则F(a,﹣
),则F(a,﹣![]() a+
a+![]() )则可得 PF=﹣
)则可得 PF=﹣![]() a2+
a2+![]() a,继而得S△PBC=﹣
a,继而得S△PBC=﹣![]() a2+
a2+![]() a,根据二次函数的性质可得当a=
a,根据二次函数的性质可得当a=![]() 时,S△PBC最大,可得点P坐标,由直线BC的解析式为y=﹣
时,S△PBC最大,可得点P坐标,由直线BC的解析式为y=﹣![]() x+
x+![]() 可得∠CBO=30°,继而可得PE+
可得∠CBO=30°,继而可得PE+![]() BE=PE+EN,根据两点之间线段最短和垂线段最短,则当P,E,N三点共线且垂直于x轴时,PE+
BE=PE+EN,根据两点之间线段最短和垂线段最短,则当P,E,N三点共线且垂直于x轴时,PE+![]() BE值最小,据此即可求得答案;
BE值最小,据此即可求得答案;
(3)由题意可得D(1,0),G(![]() ,
,![]() ),继而可得直线DG解析式,根据抛物线y=﹣
),继而可得直线DG解析式,根据抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() =﹣
=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,可得y'═﹣
沿x轴正方向平移得到新抛物线y′,y′经过点D,可得y'═﹣![]() (x+1)2+
(x+1)2+![]() ,从而可得对称轴为x=﹣1,然后分∠QDG=90°或∠QGD=90°,∠GQD=90°三种情况进行讨论即可得.
,从而可得对称轴为x=﹣1,然后分∠QDG=90°或∠QGD=90°,∠GQD=90°三种情况进行讨论即可得.
(1)当x=0时,y=﹣![]() x2+
x2+![]() x+
x+![]() =
=![]() ,
,
∴点C的坐标为(0,![]() );
);
当y=0时,有﹣![]() x2+
x2+![]() x+
x+![]() =0,
=0,
解得:x1=﹣1,x2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx+b(k≠0),
将B(3,0)、C(0,![]() )代入y=kx+b,得:
)代入y=kx+b,得:
![]() ,解得:
,解得: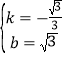 ,
,
∴直线BC的解析式为y=﹣![]() x+
x+![]() ;
;
(2)如图2中,过点P作PM⊥x轴于点M,交直线BC于点F,过点E作EN⊥x轴于点N,
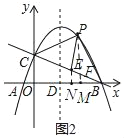
设P(a,﹣![]() a2+
a2+![]() a+
a+![]() ),则F(a,﹣
),则F(a,﹣![]() a+
a+![]() ),
),
∴PF=﹣![]() a2+
a2+![]() a,
a,
∴S△PBC=![]() ×PF×3=﹣
×PF×3=﹣![]() a2+
a2+![]() a,
a,
∴当a=![]() 时,S△PBC最大,
时,S△PBC最大,
∴P(![]() ,
,![]() ),
),
∵直线BC的解析式为y=﹣![]() x+
x+![]() ,
,
∴∠CBO=30°,EN⊥x轴,
∴EN=![]() BE,
BE,
∴PE+![]() BE=PE+EN,
BE=PE+EN,
∴根据两点之间线段最短和垂线段最短,则当P,E,N三点共线且垂直于x轴时,PE+![]() BE值最小,
BE值最小,
∴PE+![]() BE=PE+EN=PN=
BE=PE+EN=PN=![]() ;
;
(3)∵D是对称轴直线x=1与x轴的交点,G是BC的中点,
∴D(1,0),G(![]() ,
,![]() ),
),
∴直线DG解析式y=![]() x﹣
x﹣![]() ,
,
∵抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() =﹣
=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,
沿x轴正方向平移得到新抛物线y′,y′经过点D,
∴y'═﹣![]() (x+1)2+
(x+1)2+![]() ,
,
∴对称轴为x=﹣1,
∵△FGQ为直角三角形,
∴∠QDG=90°或∠QGD=90°,∠GQD=90°(不合题意,舍去),
当∠QDG=90°,设直线QD解析式y=﹣![]() x+b,过D(1,0),
x+b,过D(1,0),
∴0=﹣![]() +b,
+b,
b=![]() ,
,
∴y=﹣![]() x+
x+![]() ,
,
当x=﹣1时,y=![]() ,
,
∴Q(﹣1,![]() ),
),
当∠QGD=90°,则直线QD解析式y=﹣![]() x+
x+![]() ,
,
∴当x=﹣1时,y=![]() ,
,
∴Q(﹣1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提升学生的阅读能力,开拓学生的视野,学校开展了为期一个月的“阳光读书”活动.为了解同学们的阅读情况,校学生会随机抽取了一部分学生进行调查,并将统计数据制成如下统计图,其中A﹣﹣散文类,B﹣﹣传记类,C﹣﹣小说类,D﹣﹣期刊类,E﹣﹣其他,请你根据统计图解答以下问题:

(1)扇形统计图中D部分所对应扇形的圆心角为 度;请补全条形统计图
(2)现从A中抽选1名女同学;再从C中抽选3名同学,其中恰好有1名男同学.现准备从抽选出来的这4名同学中随机选出2名同学代表学校参加比赛,请利用画树状图或列表的方法求出选出的同学都是女同学的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+b(a≠0)的图象与x轴、y轴分别交于点B、C,与反比例函数y=

 (m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(1)求反比例函数和一次函数的解析式;
(2)求△BOD的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上一点,满足CF⊥CP,过点B作BM⊥CF,分别交AC、CF于点M、N
(1)若AC=
 AP,AC=4
AP,AC=4 ,求△ACP的面积;
,求△ACP的面积;(2)若BC=MC,证明:CP﹣BM=2FN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为
 (小时),两车之间的距离为
(小时),两车之间的距离为 (千米),图中的折线表示
(千米),图中的折线表示 与
与 之间的函数关系。
之间的函数关系。根据图象回答下列问题:

(1)甲地与乙地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需_______小时,普通列车的速度是______千米/小时;
(3)动车的速度是________千米/小时;
(4)
 的值为________.
的值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经知道,形如
 的无理数的化简要借助平方差公式:
的无理数的化简要借助平方差公式:例如:
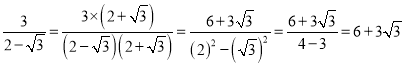 。
。下面我们来看看完全平方公式在无理数化简中的作用。
问题提出:
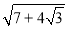 该如何化简?
该如何化简?建立模型:形如
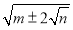 的化简,只要我们找到两个数
的化简,只要我们找到两个数 ,使
,使 ,这样
,这样 ,
, ,那么便有:
,那么便有: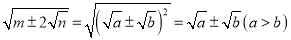 ,
,问题解决:化简
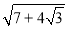 ,
,解:首先把
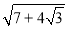 化为
化为 ,这里
,这里 ,
, ,由于4+3=7,
,由于4+3=7, ,
,即(
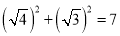 ,
, ,
,∴

模型应用1:
利用上述解决问题的方法化简下列各式:
(1)
 ;(2)
;(2) ;
;模型应用2:
(3)在
 中,
中, ,
, ,
, ,那么
,那么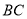 边的长为多少?(结果化成最简)。
边的长为多少?(结果化成最简)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象分别与
的图象分别与 轴和
轴和 轴交于
轴交于 ,
, 两点,且与正比例函数
两点,且与正比例函数 的图象交于点
的图象交于点 .
.
(1)求
 的值;
的值;(2)求正比例函数的表达式;
(3)点
 是一次函数图象上的一点,且
是一次函数图象上的一点,且 的面积是3,求点
的面积是3,求点 的坐标;
的坐标;(4)在
 轴上是否存在点
轴上是否存在点 ,使
,使 的值最小?若存在,求出点
的值最小?若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
相关试题

