【题目】如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上一点,满足CF⊥CP,过点B作BM⊥CF,分别交AC、CF于点M、N
(1)若AC=![]() AP,AC=4
AP,AC=4![]() ,求△ACP的面积;
,求△ACP的面积;
(2)若BC=MC,证明:CP﹣BM=2FN.

参考答案:
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由正方形的性质得出AD=CD=5,∠ADC =90°,根据勾股定理以及AC的长可求得AD=CD=4,再根据AC=![]() AP求出AP长,即可求出S△ACP;
AP求出AP长,即可求出S△ACP;
(2)在CF上截取FN=NG,连接BG,由已知可证得△BCF≌△DCP,可得CF=CP,继而可证得△BCG≌△ABM,可得BM=CG,结合图形即可推导得出CP﹣BM=2FN.
(1)∵四边形ABC是正方形,
∴AD= CD,∠ADC =90°,
∴AC=![]() ,
,
∵AC=4![]() ,
,
∴AD=CD=4,
∵AC=![]() AP,
AP,
∴AP=![]() ,
,
∴S△ACP=![]() AP×CD
AP×CD
=![]() ×
×![]() ×4
×4
=7![]() ;
;
(2)在CF上截取FN=NG,连接BG,
∵四边形ABCD是正方形,
∴AB=CB=CD,
∠CBF=∠CDP=∠BCF+∠FCD=90°,
又∵CF⊥CP,
∴∠DCP+∠FCD=90°,
∴∠BCF=∠BCD,
在△BCF和△DCP中,
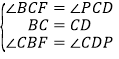 ,
,
∴△BCF≌△DCP,
∴CF=CP,
∵BC=MC,BM⊥CF,
∴∠BCF=∠ACF=![]() ∠BCA=22.5°,
∠BCA=22.5°,
∴∠CFB=67.5°,
∵FC⊥BM,FN=NG,
∴BF=BG,
∴∠FBG=45°,∠FBN=22.5°,
∴∠CBG=45°,
在△BCG和△BAN中,
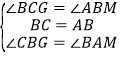 ,
,
∴△BCG≌△ABM,
∴BM=CG,
∴CF﹣CG=FG,
∵BF=BG,BM⊥CF,
∴FN=NG,
∴CP﹣BM=2FN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OA=2,OB=4,以A点为顶点,AB为腰,在第三象限作等腰Rt△ABC.

(1)求C点的坐标及△ABC的面积;
(2)如图2,P为y轴负半轴上一个动点,当P点在y轴负半轴上向下运动时,若以P为直角顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求证:OP=DE+2.
(3)已知点F坐标为(-2,-2),当G在y轴的负半轴上沿负方向运动时,请在图3作出等腰Rt△FGH,且始终保持∠GFH=90°,若FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0), 当G在y轴的负半轴上沿负方向运动时,以下结论:①m-n为定值;②m+n为定值,请判断其中哪些结论是正确的,并求出其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提升学生的阅读能力,开拓学生的视野,学校开展了为期一个月的“阳光读书”活动.为了解同学们的阅读情况,校学生会随机抽取了一部分学生进行调查,并将统计数据制成如下统计图,其中A﹣﹣散文类,B﹣﹣传记类,C﹣﹣小说类,D﹣﹣期刊类,E﹣﹣其他,请你根据统计图解答以下问题:

(1)扇形统计图中D部分所对应扇形的圆心角为 度;请补全条形统计图
(2)现从A中抽选1名女同学;再从C中抽选3名同学,其中恰好有1名男同学.现准备从抽选出来的这4名同学中随机选出2名同学代表学校参加比赛,请利用画树状图或列表的方法求出选出的同学都是女同学的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+b(a≠0)的图象与x轴、y轴分别交于点B、C,与反比例函数y=

 (m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(1)求反比例函数和一次函数的解析式;
(2)求△BOD的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=﹣
 x2+
x2+ x+
x+ 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+
 BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+ BE的最小值;
BE的最小值;(3)如图3,点G是线段CB的中点,将抛物线y=﹣
 x2+
x2+ x+
x+ 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为
 (小时),两车之间的距离为
(小时),两车之间的距离为 (千米),图中的折线表示
(千米),图中的折线表示 与
与 之间的函数关系。
之间的函数关系。根据图象回答下列问题:

(1)甲地与乙地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需_______小时,普通列车的速度是______千米/小时;
(3)动车的速度是________千米/小时;
(4)
 的值为________.
的值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经知道,形如
 的无理数的化简要借助平方差公式:
的无理数的化简要借助平方差公式:例如:
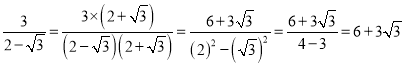 。
。下面我们来看看完全平方公式在无理数化简中的作用。
问题提出:
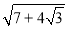 该如何化简?
该如何化简?建立模型:形如
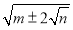 的化简,只要我们找到两个数
的化简,只要我们找到两个数 ,使
,使 ,这样
,这样 ,
, ,那么便有:
,那么便有: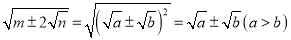 ,
,问题解决:化简
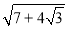 ,
,解:首先把
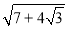 化为
化为 ,这里
,这里 ,
, ,由于4+3=7,
,由于4+3=7, ,
,即(
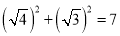 ,
, ,
,∴

模型应用1:
利用上述解决问题的方法化简下列各式:
(1)
 ;(2)
;(2) ;
;模型应用2:
(3)在
 中,
中, ,
, ,
, ,那么
,那么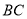 边的长为多少?(结果化成最简)。
边的长为多少?(结果化成最简)。
相关试题

