【题目】为了提升学生的阅读能力，开拓学生的视野，学校开展了为期一个月的“阳光读书”活动．为了解同学们的阅读情况，校学生会随机抽取了一部分学生进行调查，并将统计数据制成如下统计图，其中A﹣﹣散文类，B﹣﹣传记类，C﹣﹣小说类，D﹣﹣期刊类，E﹣﹣其他，请你根据统计图解答以下问题：

（1）扇形统计图中D部分所对应扇形的圆心角为　 　度；请补全条形统计图

（2）现从A中抽选1名女同学；再从C中抽选3名同学，其中恰好有1名男同学．现准备从抽选出来的这4名同学中随机选出2名同学代表学校参加比赛，请利用画树状图或列表的方法求出选出的同学都是女同学的概率

参考答案：

【答案】(1) 108，图形见解析；（2）

【解析】

（1）根据A的人数以及所占百分比求得抽取的总人数，然后减去其余各组的人数可求得D组的人数，据此可补全条形图，用D组所占的比例乘以360度即可求得相应圆心角的度数；

（2）画树状图得到所有等可能的情况，然后找出符合条件的情况数，利用概率公式进行计算即可得.

（1）抽取的总人数=20÷10%=200（名），D组人数=200﹣20﹣15﹣75﹣30=60（名）

扇形统计图中D部分所对应扇形的圆心角为=360°×=108°，

条形统计图如图所示：

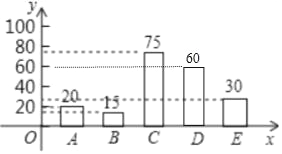
故答案为：108．

（2）画树状图得：

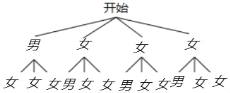
∵共有12种等可能的结果，选出的2名学生中恰好是女生的有6种情况，

∴P（2个女生）=．

关闭