【题目】一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 之间的函数关系。
之间的函数关系。
根据图象回答下列问题:

(1)甲地与乙地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需_______小时,普通列车的速度是______千米/小时;
(3)动车的速度是________千米/小时;
(4)![]() 的值为________.
的值为________.
参考答案:
【答案】(1)1200;4;(2)12;100;(3)200;(4)6.
【解析】
(1)初始时刻y=1200,即为两地距离,相遇时两车距离为0,由图像得到相遇时刻;
(2)最后到达的为普通列车,根据路程除以时间可得速度;
(3)设动车速度a千米/小时,由4小时相遇,列出方程可求解;
(4)t时刻是动车到达乙地的时刻,用路程除以速度即可.
(1)由图像可知,甲地与乙地相距1200千米,两车出发后4小时相遇;
(2)普通列车12小时到达,则速度为1200÷12=100千米/小时
(3)设动车速度a千米/小时,由题意得![]() ,
,
解得![]() ,所以动车的速度是200千米/小时;
,所以动车的速度是200千米/小时;
(4)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+b(a≠0)的图象与x轴、y轴分别交于点B、C,与反比例函数y=

 (m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(m>0)分别交于点A、B.已知A(﹣8,y0),D(x0,4),tan∠BOA=
(1)求反比例函数和一次函数的解析式;
(2)求△BOD的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上一点,满足CF⊥CP,过点B作BM⊥CF,分别交AC、CF于点M、N
(1)若AC=
 AP,AC=4
AP,AC=4 ,求△ACP的面积;
,求△ACP的面积;(2)若BC=MC,证明:CP﹣BM=2FN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=﹣
 x2+
x2+ x+
x+ 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+
 BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+ BE的最小值;
BE的最小值;(3)如图3,点G是线段CB的中点,将抛物线y=﹣
 x2+
x2+ x+
x+ 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经知道,形如
 的无理数的化简要借助平方差公式:
的无理数的化简要借助平方差公式:例如:
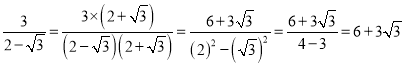 。
。下面我们来看看完全平方公式在无理数化简中的作用。
问题提出:
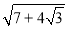 该如何化简?
该如何化简?建立模型:形如
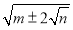 的化简,只要我们找到两个数
的化简,只要我们找到两个数 ,使
,使 ,这样
,这样 ,
, ,那么便有:
,那么便有: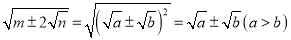 ,
,问题解决:化简
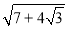 ,
,解:首先把
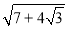 化为
化为 ,这里
,这里 ,
, ,由于4+3=7,
,由于4+3=7, ,
,即(
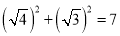 ,
, ,
,∴

模型应用1:
利用上述解决问题的方法化简下列各式:
(1)
 ;(2)
;(2) ;
;模型应用2:
(3)在
 中,
中, ,
, ,
, ,那么
,那么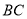 边的长为多少?(结果化成最简)。
边的长为多少?(结果化成最简)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象分别与
的图象分别与 轴和
轴和 轴交于
轴交于 ,
, 两点,且与正比例函数
两点,且与正比例函数 的图象交于点
的图象交于点 .
.
(1)求
 的值;
的值;(2)求正比例函数的表达式;
(3)点
 是一次函数图象上的一点,且
是一次函数图象上的一点,且 的面积是3,求点
的面积是3,求点 的坐标;
的坐标;(4)在
 轴上是否存在点
轴上是否存在点 ,使
,使 的值最小?若存在,求出点
的值最小?若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果,所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
相关试题

