Question

【题目】如图，已知正方形OABC的边长为2，顶点A，C分别在x轴，y轴的正半轴上，点E是BC的中点，F是AB延长线上一点且FB＝1.

（1）求经过点O，A，E三点的抛物线解析式；

（2）点P在抛物线上运动，当点P运动到什么位置时△OAP的面积为2，请求出点P的坐标；

（3）在抛物线上是否存在一点Q，使△AFQ是等腰直角三角形？若存在直接写出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝－2x2＋4x（2）(1，2)，(1＋，－2)或(1－，－2)（3）抛物线上存在点Q(， )使△AFQ是等腰直角三角形

【解析】试题分析：（1）根据点A、点E的坐标，设出二次函数的解析式，待定系数即可；

（2）判断出面积为2时的点的纵坐标，代入函数可求P点的坐标；

（3）根据题意，分三种情况讨论解答.

试题解析：(1)点A的坐标是(2，0)，点E的坐标是(1，2)．

设抛物线的解析式是y＝ax2＋bx＋c，根据题意，得

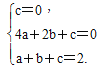
解得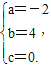

∴抛物线的解析式是y＝－2x2＋4x.

(2)当△OAP的面积是2时，点P的纵坐标是2或－2.

当－2x2＋4x＝2时，解得x＝1，

∴点P的坐标是(1，2)；

当－2x2＋4x＝－2时，解得x＝1±，

此时点P的坐标是(1＋，－2)或(1－，－2)．

综上，点P的坐标为(1，2)，(1＋，－2)或(1－，－2)．

(3)∵AF＝AB＋BF＝2＋1＝3，OA＝2.

则点A是直角顶点时，Q不可能在抛物线上；

当点F是直角顶点时，Q不可能在抛物线上；

当点Q是直角顶点时，Q到AF的距离是AF＝，若点Q存在，则Q的坐标是(， )．将Q(， )代入抛物线解析式成立．

∴抛物线上存在点Q(， )使△AFQ是等腰直角三角形．